1 ディリクレ積分
複素数の教科書に例として載っていることが多いと思いますが,
\[ \int_0^\infty \frac{\sin(x)}{x} = \frac{\pi}{2} \]
の証明を確認していきましょう.
複素関数\(f(z) = \exp(iz) / z\)の以下の積分路\(C\)の値を考えます。
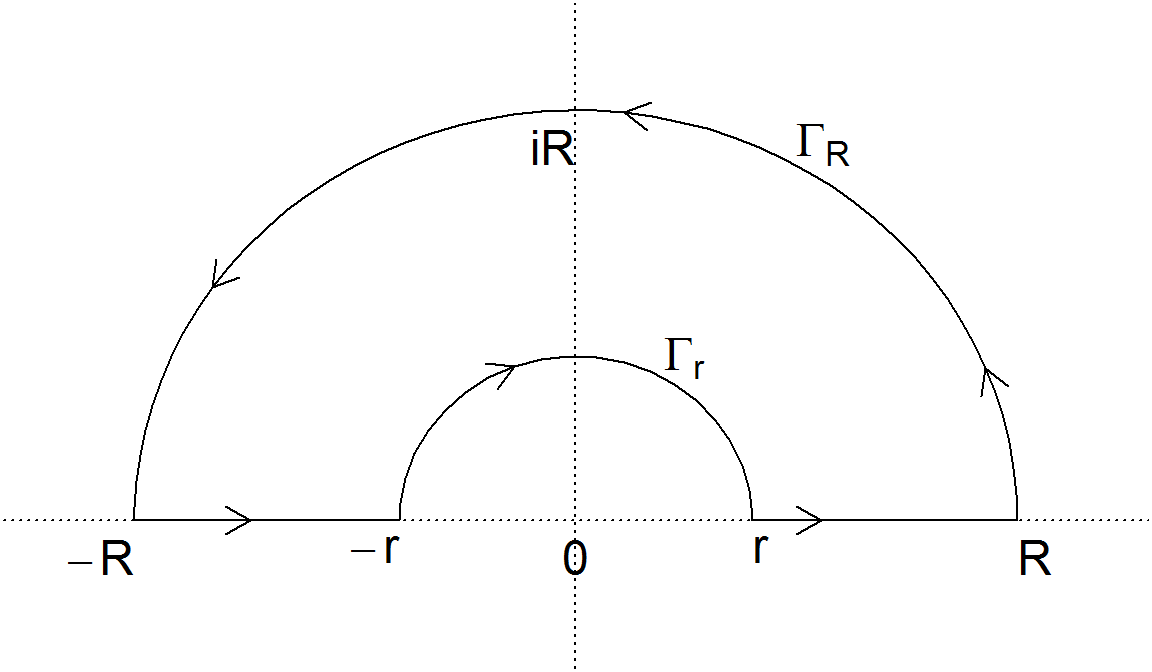
特異点\(z=0\)は閉路の外側にあるので,コーシーの積分定理によりこの積分は\(0\)となります.
\[ \oint_C \frac{e^{iz}}{z} dz = 0 \]
積分路\(C\)は\([-R, -r)\),\(\Gamma_r\),\([r, R]\),\(\Gamma_R\)の4区間に分割でき,それぞれの積分することができます.
\[ \oint_C \frac{e^{iz}}{z} dz = \int_{-R}^{-r} \frac{e^{ix}}{x} dx + \int_{\Gamma_r} \frac{e^{iz}}{z} dz + \int_{r}^{R} \frac{e^{ix}}{x} dx + \int_{\Gamma_R} \frac{e^{iz}}{z} dz \]
実軸上の積分をまとめます.
\[ \begin{align*} &= \int_{r}^{R} \frac{e^{i(-x)}}{-x} (-1) dx + \int_{r}^{R} \frac{e^{ix}}{x} dx + \int_{\Gamma_r} \frac{e^{iz}}{z} dz + \int_{\Gamma_R} \frac{e^{iz}}{z} dz \\ &= \int_{r}^{R} \frac{e^{i(-x)} + e^{ix}}{x} dx + \int_{\Gamma_r} \frac{e^{iz}}{z} dz + \int_{\Gamma_R} \frac{e^{iz}}{z} dz \\ &= 2i \int_{r}^{R} \frac{\sin(x)}{x} dx + \int_{\Gamma_r} \frac{e^{iz}}{z} dz + \int_{\Gamma_R} \frac{e^{iz}}{z} dz \end{align*} \]
整理します.
\[ \int_{r}^{R} \frac{\sin(x)}{x} dx = \frac{-1}{2i} \bigg[ \int_{\Gamma_r} \frac{e^{iz}}{z} dz + \int_{\Gamma_R} \frac{e^{iz}}{z} dz \bigg] \]
\(r \rightarrow 0\),\(R \rightarrow \infty\)とすれば,求める値になります.
内側の円の区間\(\Gamma_r\)の積分は,\(e^{iz}\)をマクローリン展開すると
\[ \begin{align*} \lim_{r \rightarrow 0} \int_{\Gamma_r} \frac{e^{iz}}{z} &= \lim_{r \rightarrow 0} \int_{\Gamma_r} \frac{1}{z} \bigg( 1 + iz - \frac{z^2}{2!} + i\frac{z^3}{3!} + \cdots \bigg) dz \\ &= \lim_{r \rightarrow 0} \int_{\Gamma_r} \frac{1}{z} \bigg( 1 + \sum_{n=1}^{\infty} \frac{i^nz^n}{n!} \bigg) dz\\ \end{align*} \]
\(z = re^{i\theta}\)と変数変換すると
\[ \begin{align*} &= \lim_{r \rightarrow 0} \int_{\pi}^0 \frac{1}{re^{i\theta}} \bigg( 1 + \sum_{n=1}^{\infty} \frac{i^n(i re^{i\theta})^n}{n!} \bigg) i r e^{i\theta} d\theta \\ &= \lim_{r \rightarrow 0} i \int_{\pi}^0 \bigg( 1 + \sum_{n=1}^{\infty} \frac{(-1)^n r^n (e^{i\theta})^n}{n!} \bigg) d\theta \\ &= \lim_{r \rightarrow 0} \bigg( i \int_{\pi}^0 1 d\theta + \sum_{n=1}^{\infty} \int_{\pi}^0 i \frac{(-1)^n r^n (e^{i\theta})^n}{n!} d\theta \bigg) \\ &= \lim_{r \rightarrow 0} \bigg( i \big[ \theta \big]_{\pi}^0 + \sum_{n=1}^{\infty} \bigg[ \frac{(-1)^n r^n (e^{i\theta})^{n+1}}{n!(n+1)} \bigg]_{\pi}^0 \bigg) \\ &= \lim_{r \rightarrow 0} \bigg( -i\pi + \sum_{n=1}^{\infty} \frac{(-1)^nr^n(1 - (-1)^{n+1})}{n!(n+1)} \bigg) \\ &= -i\pi + 0 \end{align*} \]
外側の円の区間\(\Gamma_R\)の積分は,\(z=Re^{i\theta}\)と置いて,森・杉原『複素関数論』の補題7.3を使うか,
\[ \begin{align*} \bigg|\int_{\Gamma_R}\frac{e^iz}{z}dz\bigg| &= \bigg| \int_0^\pi \frac{e^{iRe^{i\theta}}}{Re^i\theta} iRe^i\theta d\theta \bigg| \\ &= \bigg| \int_0^\pi e^{iR(\cos(\theta)+i\sin(\theta))} i d\theta \bigg| \\ &= \bigg| \int_0^\pi e^{iR\cos(\theta)}e^{-R\sin(\theta)} i d\theta \bigg| \\ &\le \int_0^\pi \bigg|e^{iR\cos(\theta)}\bigg|\bigg|e^{-R\sin(\theta)}\bigg|\bigg| i \bigg| d\theta \\ &= \int_0^\pi \bigg|e^{-R\sin(\theta)}\bigg| d\theta \\ &\le \int_0^\pi \bigg|e^{-R\theta}\bigg| d\theta \\ &= \bigg[ \frac{e^{-R\theta}}{-R} \bigg]_0^\pi = \frac{1 - e^{-R\pi}}{R}\\ \end{align*} \]
から,
\[ \lim_{R \rightarrow \infty} \int_{\Gamma_R} \frac{e^{iz}}{z} = 0 \]
になります.
よって
\[ \int_{0}^{\infty} \frac{\sin(x)}{x} dx = \frac{-1}{2i} \bigg[ -i\pi + 0 \bigg] = \frac{\pi}{2} \]
2 テント関数の定義
図を見たら名前の由来が分かります.
\[ T(x) = \begin{cases} x + 1 & -1 \le x \le 0 \\ -x + 1 & 0 \le x \le 1 \\ 0 & \mathrm{elsewhere} \end{cases} \]
\[ T_{a,b,c}(x) = c T\bigg(\frac{2}{b - a}\big(x - \frac{a + b}{2}\big)\bigg) \quad (a \le b,\ c \ge 0) \]

3 テント関数の特性関数
\(U,V \sim U(0, a)\)のとき,\(U-V\)の確率密度関数は\(T_{-a, a, 1/a}\)となります.
\(U-V\)の累積分布関数を考えます.
\[ \begin{align*} F(t) &= P(U-V \le t) \\ &= \begin{cases} 0 & t \lt -a \\ \frac{1}{2a^2}(a^2 + t^2) + \frac{t}{a} & -a \le t \lt 0 \\ \frac{1}{2a^2}(a^2 - t^2) + \frac{t}{a} & 0 \le t \le a \\ 1 & t \gt a \end{cases} \end{align*} \]
なぜならば,
\[ \begin{align*} F(t) &= P(U-V \le t) \\ &= \int_0^a \frac{1}{a} \int_0^a \frac{1}{a} 1_{(-\infty, t]}(u - v) du dv \\ &= \frac{1}{a^2} \int_0^a \int_0^a 1_{(-\infty, t]}(u - v) du dv\\ &= \frac{1}{a^2} \int_0^a \int_0^a 1_{(-\infty, t+v]}(u) du dv \end{align*} \]
\(0 \le t \le a\)のとき
\[ \begin{align*} F(t) &= \frac{1}{a^2} \int_0^a \mathrm{min}(t+v, a) dv \\ &= \frac{1}{a^2} \bigg[ \frac{1}{2}(t+v)^2 \bigg]_0^{a-t} + \frac{t}{a} \\ &= \frac{1}{2a^2}(a^2 - t^2) + \frac{t}{a} \end{align*} \]
\(-a \le t \le 0\)のとき
\[ \begin{align*} F(t) &= \frac{1}{a^2} \int_0^a \mathrm{max}(t+v, 0) dv \\ &= \frac{1}{a^2} \int_{-t}^{a} t + v \ dv \\ &= \frac{1}{2a^2}(a^2 + t^2) + \frac{t}{a} \end{align*} \]
累積分布関数を微分した確率密度関数は
\[ \begin{align*} F'(t) &= \begin{cases} \frac{1}{a^2}(a + t) & \ -a \lt t \lt 0 \\ \frac{1}{a^2}(a - t) & \ 0 \le t \lt a \end{cases} \\ &= \frac{1}{a^2}(a - |t|) \\ &= T_{-a,a,1/a}(t) \end{align*} \]
\(T_{-a,a,1/a}\)は\(U-V\)と同値であるため,特性関数も同じです. \(\exp(iaz) = \cos(az) + i\sin(az)\)に注意して,
\[ \begin{align*} \int e^{izx}T_{-a,a,1/a}(x)\ dx &= \int_0^a \int_0^a \frac{1}{a^2} e^{iz(u-v)}\ dudv \\ &= \frac{e^{iaz} - 1}{iaz} \cdot \frac{e^{-iaz} - 1}{-iaz} \\ &= \frac{2 - e^{iaz} - e^{-iaz}}{a^2z^2} \\ &= \frac{2}{a^2z^2}(1 - \cos(az)) \end{align*} \]
4 テント関数の期待値
確率変数Xの特性関数を\(\varphi_X\)とするとき
\[ \begin{align*} E\big[T(X)\big] = \frac{1}{\pi} \int_{-\infty}^{\infty} \varphi_X(z) \frac{1 - \cos(az)}{z^2}\ dz \\ E\big[T_{a,b,c}(X)\big] = \frac{2c}{\pi(b-a)}\int_{-\infty}^{\infty} \varphi_X(z) e^{-i\frac{(a+b)z}{2}} \frac{1 - \cos(\frac{b-a}{2}z)}{z^2}\ dz \end{align*} \]
なぜならば,\(T(x)=T_{1,1,1}(x)\)なので,
\[ \begin{align*} \int_{-\infty}^{\infty} e^{izx} T(x) dz = \frac{2(1 - \cos(z))}{z^2} \end{align*} \]
また,
\[ \begin{align*} \int_{-\infty}^{\infty} e^{izx} \frac{2(1 - \cos(z))}{z^2} dz = \pi T(x) \end{align*} \]
なぜならば,\((1-\cos(z))/z^2\)が偶関数なので,\(\exp(izx) = \cos(zx) + i\sin(zx)\)で,\(\int i\sin(zx) (1-\cos(z))/z^2 dz = 0\)になることに注意すると
\[ \begin{align*} \int_{-\infty}^{\infty} e^{izx} \frac{2(1 - \cos(z))}{z^2} dz = \int_{-\infty}^{\infty} \cos(zx) \frac{2(1 - \cos(z))}{z^2} dz \end{align*} \]
また
\[ \begin{align*} \cos(z(x+1)) &= \cos(zx)\cos(z) - \sin(zx)\sin(z)\\ \cos(z(x-1)) &= \cos(zx)\cos(z) + \sin(zx)\sin(z)\\ \cos(z(x+1)) + \cos(z(x-1)) &= 2\cos(zx)\cos(z) \end{align*} \]
なので,
\[ \cos(zx)(1-\cos(z)) = \cos(zx) - \frac{1}{2}(\cos(z(x+1)) + \cos(z(x-1))) \]
だから,
\[ \begin{align*} \int_{-\infty}^{\infty} e^{izx} \frac{2(1 - \cos(z))}{z^2} dz &= \int_{-\infty}^{\infty} e^{izx} \frac{2(1 - \cos(z))}{z^2} dz \end{align*} \]
\[ \begin{align*} &= \int_{-\infty}^{\infty} \cos(zx) - \frac{1}{2}(\cos(z(x+1)) + \cos(z(x-1))) dz \\ &= \int_{-\infty}^{\infty} \frac{1 - \cos(zx)}{z^2} dz - \frac{1}{2} \int_{-\infty}^{\infty} \frac{1 - \cos(z(x+1))}{z^2} dz - \frac{1}{2} \int_{\infty}^{-\infty} \frac{1 - \cos(z(x-1))}{z^2} dz \end{align*} \]
右辺第1項を\(\xi=-z|x|\),第2項を\(\xi=-z|x+1|\),第3項を\(\xi=-z|x-1|\)で変数変換をすると
\[ \begin{align*} \int_{-\infty}^{\infty} \frac{1 - \cos(zx)}{z^2} dz &= \int_{\infty}^{-\infty} \frac{1 - \cos(-\xi)}{(-\xi)^2} |x|^2 \frac{-1}{|x|} d\xi \\ &= - |x| \int_{\infty}^{-\infty} \frac{1 - \cos(-\xi)}{(-\xi)^2} d\xi \\ &= - |x| \int_{-\infty}^{\infty} \frac{1 - \cos(\xi)}{\xi^2} d\xi \end{align*} \]
\[ \begin{align*} \frac{1}{2} \int_{-\infty}^{\infty} \frac{1 - \cos(z(x+1))}{z^2} dz &= - \frac{1}{2} |x + 1| \int_{-\infty}^{\infty} \frac{1 - \cos(\xi)}{\xi^2} d\xi \\ \frac{1}{2} \int_{-\infty}^{\infty} \frac{1 - \cos(z(x-1))}{z^2} dz &= - \frac{1}{2} |x - 1| \int_{-\infty}^{\infty} \frac{1 - \cos(\xi)}{\xi^2} d\xi \end{align*} \]
合成関数の積分とディリクレ積分の結果を用いると
\[ \begin{align*} \int_{-\infty}^{\infty} \frac{1 - \cos(z)}{z^2} dz &= \bigg[ \frac{-(1-\cos(z))}{z}\bigg]_{\infty}^{\infty} + \int_{-\infty}^{\infty} \frac{\sin(z)}{z} dz \\ &= 0 + 2 \int_0^\infty \frac{\sin(z)}{z} dz \\ &= \pi \end{align*} \]
これらの式で整理すると
\[ \begin{align*} \int_{-\infty}^{\infty} e^{izx} \frac{2(1 - \cos(z))}{z^2} dz &= \pi \bigg( \frac{1}{2}|x+1| + \frac{1}{2}|x-1| - |x| \bigg) = \pi T(x) \end{align*} \]
よって\(T(X)\)の期待値を計算すると
\[ \begin{align*} E[T(X)] &= \frac{1}{\pi} E\bigg[ \int_{-\infty}^{\infty} e^{izX} \frac{2(1 - \cos(z))}{z^2} dz \bigg] \\ &= \frac{1}{\pi} \int_{-\infty}^{\infty} E\big[ e^{izX} \big] \frac{2(1 - \cos(z))}{z^2} dz\\ &= \frac{1}{\pi} \int_{-\infty}^{\infty} \varphi_X(z) \frac{2(1 - \cos(z))}{z^2} dz \end{align*} \]
さらに
\[ \varphi_{\frac{2}{b-a}\big(X - \frac{a+b}{2}\big)} = \varphi_X\bigg(\frac{2z}{b-a}\bigg)e^{-i\frac{a+b}{b-a}} \]
に注意すれば
\[ E\big[T_{a,b,c}(X) \big] = \frac{c}{\pi} \int_{-\infty}^{\infty} \varphi_X\big( \frac{2z}{b-a} \big) e^{-i\frac{a+b}{b-a}} \frac{2(1 - \cos(z))}{z^2} dz \]
5 台形関数の定義
名前の通りですが,\(c\)を大きくすると長方形に近づいていきます.
\[ \begin{align*} D_{a,b,c}(x) &= \mathrm{min}(T_{a,b,c}(x), 1) \\ &= T_{a,b,c}(x) - T_{a + \frac{b - a}{2c}, b - \frac{b - a}{2c}, c - 1}(x) \end{align*} \]

6 特性関数が同じならば、同じ分布
確率変数\(X, Y\)の特性関数を\(\varphi_X, \varphi_Y\)とするとき,\(\varphi_X(z) = \varphi_Y(z) \quad \forall z \in \mathbb{R}\)ならば,\(X\)と\(Y\)の分布は一致します.
なぜならば
\[ \begin{align*} E\big[ T_{a,b,c}(X) \big] &= E\big[ T_{a,b,c}(Y) \big] \\ E\big[ D_{a,b,c}(X) \big] &= E\big[ D_{a,b,c}(Y) \big] \end{align*} \]
\(\lim_{c\rightarrow \infty} D_{a,b,c}(x) = 1_{(a,b)}(x)\)となるため,\(E\big[ 1_{(a,b)}(X) \big] = P(a \lt X \lt b)\)に注意すると,
\[ P(a \lt X \lt b) = P(a \lt X \lt b) \]
となります.\(a\)と\(b\)は任意なので、\(X\)と\(Y\)の分布は一致します.
