1 ファイルの読み込みと集計
回帰分析に使うデータセットと異なり変化があるので、それぞれの場合の読み込み方を説明します。
1.1 未集計データの場合
df01 <- read.table("https://wh.anlyznews.com/R/dataset/for_xtt.csv",
header = TRUE, sep = ",",
colClasses = c("character", "factor", "factor"))2列目と3列名が因子型になるように指定しています。なお、colClassesを指定する代わりに、stringsAsFactors = TRUE, as.is = "name"を入れても同じ結果になります。
name d1 d2
1 Noah a x
2 William b z
3 Alfred b z
4 Carl c z
5 Aksel b z
6 Emil c z中身は見ての通り、3種類の文字列のデータセットです。
name d1 d2
Length:100 a:32 x:14
Class :character b:35 y:15
Mode :character c:33 z:71 因子型にしておくと、summaryで要素ごとの頻度が出ます。因子型の2列目と3列目が、今回の分析の対象となります。
ペンギンで覚えるRの集計関数で練習したように、集計してクロス表を作成します。
d2
d1 x y z
a 10 0 22
b 2 2 31
c 2 13 182 独立性の検定
十分な統制ではなく他に計量分析をかけることになるので計算しないことも多いと思いますが、表全体とセルごとの統計的仮説検定をかけるのが教科書的な方法です。
どの行かで表される因子とどの列かで表される因子が独立だとします。\(i\)行かつ\(j\)列である期待確率は、\(i\)行になる確率と\(i\)列になる確率を乗じたものになります。つまり、\(i\)行の頻度の合計と\(j\)列の頻度の合計を乗じたものを、全体の頻度の合計で二回割ったものが期待確率です。期待頻度は、それにさらに全体の頻度をかけたものになります。
観測値と期待頻度の差は二項分布に、近似的に正規分布に従います。よって、観測値と期待頻度の差を標準偏差で割って標準化した値の二乗が、χ二乗分布に従うと看做すことができます。さらに、多項分布の性質を使うと、観測値と期待頻度の差を期待頻度で割った値の二乗和が、標準化した値の二乗和と等しいことが分かり1、χ二乗検定を用いて独立性の検定を行うことができます2。また、各セルの差も正規分布を用いて外れ値でないか検定ができます3。
Warning in chisq.test(xt, correct = FALSE): カイ自乗近似は不正確かもしれません
Pearson's Chi-squared test
data: xt
X-squared = 24.373, df = 4, p-value = 6.722e-05xt_p_value <- 2*pnorm(abs(xst$stdres), lower.tail = FALSE)
(xt_adj_p_value <- matrix(p.adjust(xt_p_value), nrow(xt_p_value), dimnames = dimnames(xt_p_value))) # 多重比較補正/Holm法 x y z
a 0.01647524 0.0214869316 0.9624113
b 0.23439541 0.9624112772 0.2343954
c 0.65342761 0.0008567694 0.2343954近似が不正確かも知れないと警告されます。期待値が小さいセルがあるからです。教科書的にはfisher.testかシミュレーションの値を使うべきとなります。ただし、chisq.test(xt, simulate.p.value = TRUE, B = 1000000)と大きなサンプリングサイズのシミュレーションで値を計算しても、話が変わるようなことはほとんどないと思います。
2.1 検定統計量のプロット
ほとんど利用されていない気がしますが、χ二乗検定の検定統計量の各セルごとの値の符号付平方根がプロットができます(Cohen-Friendly association plot)。
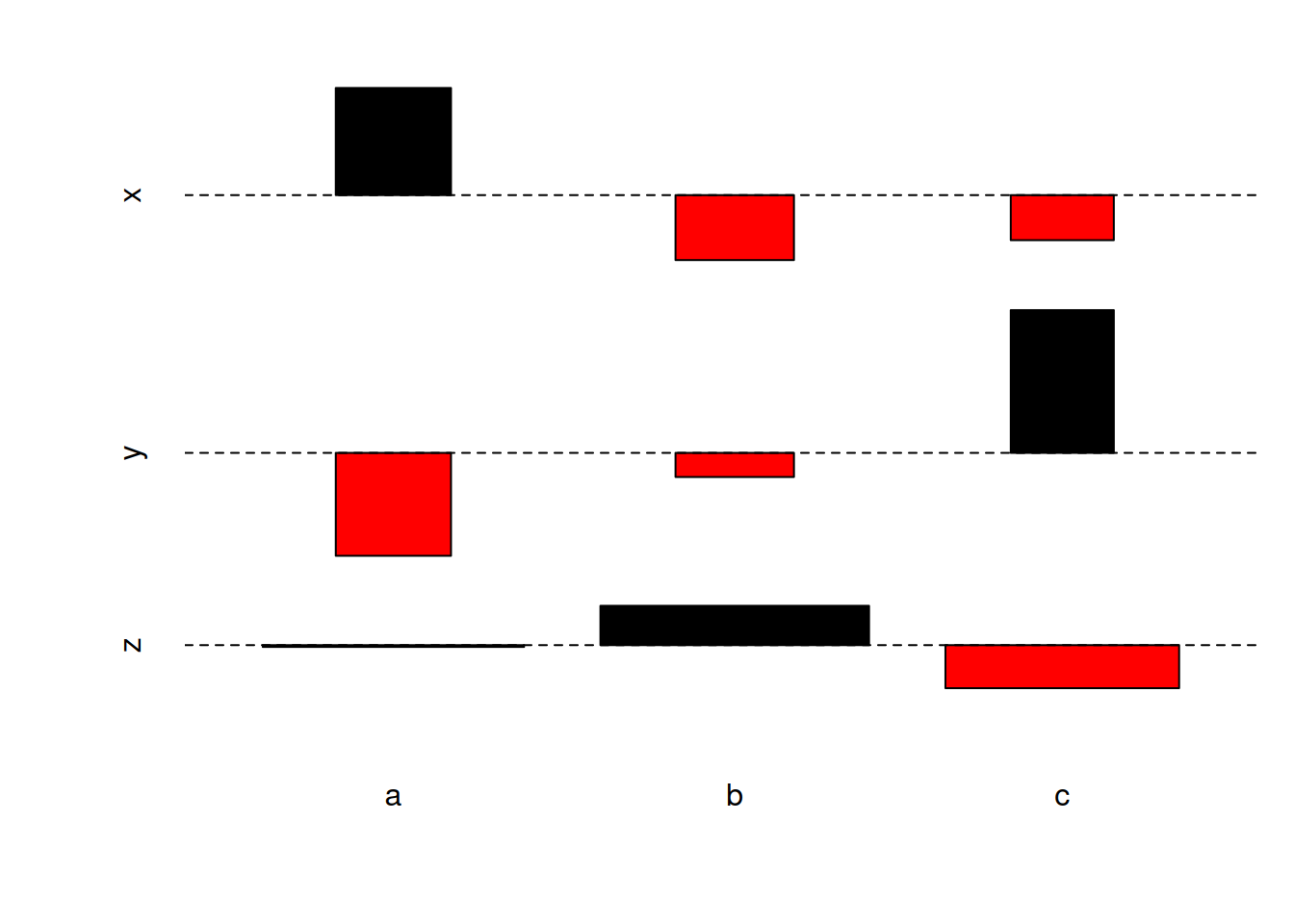
行\(i\)列\(j\)のセルの観測値を\(f_{ij}\)、期待値を\(e_{ij}\)置いて、高さが\((f_{ij} - e_{ij}) / \sqrt{e_{ij}}\)、幅が\(\sqrt{e_{ij}}\)です。χ二乗検定の検定統計量は、\(\sum_{ij} (f_{ij} - e_{ij})^2 / e_{ij}\)です。
2.2 クロス表のプロット
プロットでは無く表を画くことがほとんどですが、ヒートマップで視覚化することもできます。ただし、標準のheatmapはセルの値が表示できず、アスタリスクも入れられません。今回はimageを使って描画します。
plotXTT <- function(xt, xt.p.value = 1+1e06, pt.cex = 1.25){
M <- xt
for(i in 1:nrow(xt)){
M[i, ] <- xt[nrow(xt) - i + 1, ]
}
rownames(M) <- rev(rownames(M))
image(t(M), axes = FALSE,
col = colorRampPalette(c("white", "pink"))(max(M) + 1))
at_x <- seq(0, 1, length.out = ncol(M))
at_y <- seq(0, 1, length.out = nrow(M))
axis(1, at = at_x, labels = colnames(M), lwd = 0, lwd.ticks = 1)
axis(2, at = at_y, labels = rownames(M), lwd = 0, lwd.ticks = 1)
A <- matrix(ifelse(xt.p.value <= 0.01, "^'***'",
ifelse(xt.p.value <= 0.05, "^'**'",
ifelse(xt.p.value <= 0.10, "^'*'", "")
)
), nrow(M), ncol(M))
for(i in 1:nrow(M)){
for(j in 1:ncol(M)){
text(at_x[j], at_y[i],
parse(text = sprintf("%.0f%s", M[i, j], A[i, j])), cex = pt.cex)
}
}
}
par(mar = c(7, 4, 1, 1))
plotXTT(xt, xt_adj_p_value)
mtext("Note) ***, ** and * are statistically significant at the 1%, 5% and 10% level, respectively.", side = 1, line = par()$mgp[1] + 1, adj = 1, xpd = TRUE)
expr <- substitute(paste(chi^2, " statistic: ", s, ", DF: ", df, ", p-value: ", p), with(xst, list(s = statistic, df = parameter[["df"]], p = p.value)))
mtext(expr, side = 1, line = par()$mgp[1] + 2.5, adj = 1, xpd = TRUE)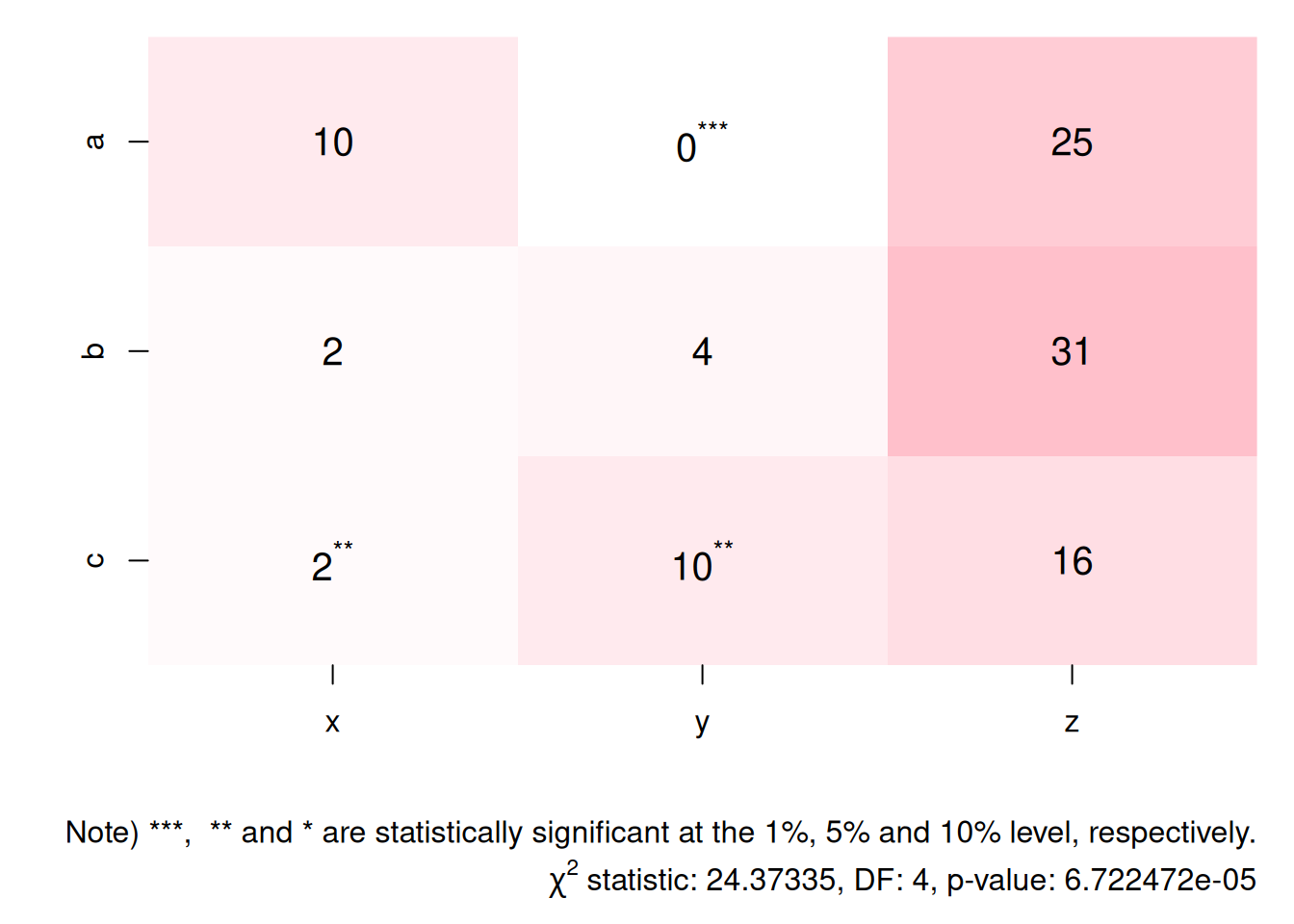
ComplexHeatmap::Heatmapで同様のことができるようです。
3 相関の強さをあらわす指標
独立性検定では相関のあるか/あると言えないかしか判定できませんが、相関係数の拡張になるCramér’s V(もしくは\(\varphi_c\))と言う指標があります。広く使われているようでは無さそうですが、概要は把握しておきましょう。
サンプルサイズ\(n\)の\(k\)行\(r\)列のクロス表の場合は、以下のように定義されます。
\[ V = \sqrt{\frac{\varphi^2}{\min(k-1, r-1)}} = \sqrt{\frac{\chi^2/n}{\min(k-1, r-1)}} \]
pwrパッケージなどで計算することが多いようですが、一行で計算できます。
[1] 0.34909423.1 バイアス補正版
相関を過剰評価しやすいようでバイアス補正したバージョンもあり、
\[\begin{align} \tilde{V} &= \sqrt{\frac{\tilde{\varphi}^2}{\min(\tilde{k}-1, \tilde{r}-1)}} \\ \tilde{\varphi}^2 &= \max\bigg( 0, \varphi^2 - \frac{(k-1)(r-1)}{n-1} \bigg) \\ \tilde{k} &= k - \frac{(k-1)^2}{n-1} \\ \tilde{r} &= r - \frac{(r-1)^2}{n-1} \end{align}\]
と定義されています。これも多少は手間ですが、
phi2 <- c(xst$statistic/sum(xt), use.names = FALSE)
t_phi2 <- max(0, phi2^2 - (nrow(xt) - 1)*(ncol(xt) - 1)/(sum(xt) - 1))
t_k <- nrow(xt) - (nrow(xt) - 1)^2/(sum(xt) - 1)
t_r <- ncol(xt) - (ncol(xt) - 1)^2/(sum(xt) - 1)
(t_V <- sqrt(t_phi2 / min(t_k - 1, t_r - 1)))[1] 0.0984728と計算できます。
3.2 ピアソンの積率相関係数との関係
2行2列のクロス表の場合は\(V\)はファイ係数と同一になり、1行1列に数えられる因子を1、2行1列に〃を0、1行2列に〃を0、2行2列に〃を1とした場合の、ピアソンの積率相関係数と一致します。
因子が1か0のデータセットをつくって試してみましょう。
set.seed(710)
n <- 100
df03 <- data.frame(x = sample(c(1, 0), n, replace = TRUE), y = sample(c(1, 0), n, replace = TRUE))
i <- round(runif(30, 0.5, n + 0.5))
head((df03 <- within(df03, y[i] <- x[i])), 5) x y
1 0 0
2 1 0
3 0 0
4 0 1
5 1 0 y
x 0 1
0 27 17
1 19 37xst <- chisq.test(xt, correct = FALSE)
sprintf("Pearson correlation coefficient: %.5f", with(df03, cor(x, y)))[1] "Pearson correlation coefficient: 0.27324"[1] "Cramér's V (Phi coefficient): 0.27324"4 信頼区間の計算
医療統計の教科書どおりに計算すれば出てきますが、コードを確認しておきましょう。
4.1 オッズ比
医療統計でよくみるオッズ比と信頼区間の計算をしましょう。
# 2×2表をつくる
M <- matrix(c(283, 145, 169, 130), 2, dimnames = list(c("men", "women"), c("negative", "positive")))
# オッズを計算
odds <- M[,2]/M[,1]
# オッズ比を計算
odds_ratio <- odds[2]/odds[1]
# 対数オッズ比の標準誤差を計算
se_log_odds <- sqrt(sum(1/M))
# 対数オッズ比の100*1-a%信頼区間を計算
a <- 0.05
interval <- c(qnorm(a/2), 0, qnorm(1-a/2))
names(interval) <- c("lower", "estimate", "upper")
log_odds_confint <- se_log_odds*interval + log(odds_ratio)
# オッズ比の信頼区間を計算
(odds_confint <- exp(log_odds_confint)) lower estimate upper
1.107895 1.501326 2.034470 対数オッズ比の分散はクロス表の4つのセルの観測数のそれぞれの逆数の和で近似することができるので、そのように計算しています。
なお、実用ではepitoolsパッケージなどを使う方がよいでしょう。2行以上の行列も処理してくれますし、独立性検定なども複数の手法で同時にやってくれます。
NA
odds ratio with 95% C.I. estimate lower upper
men 1.000000 NA NA
women 1.501326 1.107895 2.034474.2 リスク比
オッズとリスクの計算の分母が異なることに注意すれば、リスク比も同様に計算できます。
risk <- M[,2]/(M[,1] + M[,2])
risk_ratio <- risk[2]/risk[1]
se_log_risk <- sqrt(sum(1/M[1,2] + 1/M[2,2] - 1/(M[1,1] + M[1,2]) - 1/(M[2,1] + M[2,2])))
log_risk_confint <- se_log_risk*interval + log(risk_ratio)
names(log_risk_confint) <- c("lower", "estimate", "upper")
(risk_confint <- exp(log_risk_confint)) lower estimate upper
1.063839 1.264336 1.502619 これも実用では、epitoolsパッケージなどを使う方がよいでしょう。
NA
risk ratio with 95% C.I. estimate lower upper
men 1.000000 NA NA
women 1.264336 1.063839 1.5026194.3 絶対リスク差
あまり使われていないみたいですが、割り算が入らない分だけ容易に計算できます。
rd <- c(risk[2] - risk[1], use.names = FALSE)
se_rd <- sqrt(M[1,1]*M[1,2]/(M[1,1]+M[1,2])^3 + M[2,1]*M[2,2]/(M[2,1]+M[2,2])^3)
(rd_confint <- se_rd*interval + rd) lower estimate upper
0.02486461 0.09883347 0.17280232 これは実用では、ビルトインのprop.testを用いるのがよいでしょう。
2-sample test for equality of proportions without continuity correction
data: M
X-squared = 6.8976, df = 1, p-value = 0.008631
alternative hypothesis: two.sided
95 percent confidence interval:
0.02486461 0.17280232
sample estimates:
prop 1 prop 2
0.6261062 0.5272727 Benhamou and Melot (2018)に証明があります。ただしクロス表で使うには、さらに議論が必要です。↩︎
正規分布を仮定しないFisherの正確検定をかける場合は、
fisher.test(xt)です。↩︎セルごとに期待値\(e_{ij}\)が出るので、観測値を\(n\)として、多項分布の性質からセルごとに分散\(n(e_{ij}/n)(1 - e_{ij}/n)\)が出ます。↩︎
