Rによる等分散性の検定と分散分析（ANOVA）
分散分析で使われるF分布について基本的な事項を確認し、尖度による自由度補正をかける適用できる分布の条件を緩めた手法を紹介します。
1 F分布の導出
それぞれ自由度\(m\)と\(n\)のχ二乗分布に従う独立な確率変数\(X\), \(Y\)で表される
\[ z = \frac{X/m}{Y/n} \]
が従うのがF分布です。
導出には、まず、\(X\)と\(Y\)の同時確率密度を考えます。
独立なので
\[\begin{align} f_{m,n}(X, Y) &= f_m(X)f_n(Y) \\ &= \frac{X^{\frac{m}{2}-1}\exp(-\frac{X}{2})}{2^{\frac{m}{2}}\Gamma\big(\frac{m}{2}\big)} \frac{Y^{\frac{n}{2}-1}\exp(-\frac{Y}{2})}{2^{\frac{n}{2}}\Gamma\big(\frac{n}{2}\big)} \end{align}\]
となります。
\[\begin{align} z &= \frac{X/m}{Y/n} \\ y &= Y \end{align}\]
で変数変換をすると、
\[\begin{align} f_{m,n}(z, y) &= \frac{ \big(\frac{m}{n} zy \big)^{\frac{m}{2}-1} \exp\big(-\frac{mzy}{2n}\big) }{2^\frac{m}{2} \Gamma\big(\frac{m}{2}\big) } \frac{ y^{\frac{n}{2}-1}\exp\big(-\frac{y}{2}\big) }{ 2^\frac{n}{2} \Gamma\big(\frac{n}{2}\big) } \begin{vmatrix} \frac{m}{n}y & \frac{my^2}{nX} \\ 0 & 1 \end{vmatrix} \\ &= \frac{ \big( \frac{m}{n} \big)^\frac{m}{2} z^{\frac{m}{2}-1} }{ 2^\frac{m + n}{2} \Gamma\big(\frac{m}{2}\big)\Gamma\big(\frac{n}{2}\big)} y^{\frac{m+n}{2}-1}\exp\bigg(-\frac{(n+mz)y}{2n}\bigg) \end{align}\]
となります。
\(y\)で積分すると、\(z\)の確率密度関数になります。
\[\begin{align} &f_{m,n}(z) \\ &= \frac{ \big( \frac{m}{n} \big)^\frac{m}{2} z^{\frac{m}{2}-1} }{ 2^\frac{m + n}{2} \Gamma\big(\frac{m}{2}\big)\Gamma\big(\frac{n}{2}\big)} \int_0^{\infty} y^{\frac{m+n}{2}-1}\exp\bigg(-\frac{(n+mz)y}{2n}\bigg) dy \end{align}\]
この積分はガンマ関数の形に持ち込めます。つまり\(u=(mz+n)y/2n\)と変数変換します。
\[\begin{align} &= \frac{ \big( \frac{m}{n} \big)^\frac{m}{2} z^{\frac{m}{2}-1} }{ 2^\frac{m + n}{2} \Gamma\big(\frac{m}{2}\big)\Gamma\big(\frac{n}{2}\big)} \bigg( \frac{2n}{mz + n}\bigg)^\frac{m+n}{2} \int_0^{\infty} u^{\frac{m+n}{2}-1}\exp(-u) du \\ &= \frac{ \big( \frac{m}{n} \big)^\frac{m}{2} z^{\frac{m}{2}-1} }{ \Gamma\big(\frac{m}{2}\big)\Gamma\big(\frac{n}{2}\big)} \bigg( \frac{n}{mz + n}\bigg)^\frac{m+n}{2} \Gamma\bigg(\frac{m+n}{2}\bigg) \end{align}\]
ガンマ関数とベータ関数の関係を思い出して整理すると、
\[\begin{align} &=\frac{ \big( \frac{m}{n} \big)^\frac{m}{2} z^{\frac{m}{2}-1} }{ B\big(\frac{m}{2}, \frac{n}{2}\big) } z^{\frac{n}{2}-1} \bigg( \frac{n}{mz + n}\bigg)^\frac{m+n}{2} \\ f_{m,n}(z) &=\frac{ 1 }{ B\big(\frac{m}{2}, \frac{n}{2}\big) } \bigg( \frac{m}{n} \bigg)^\frac{m}{2} z^{\frac{m}{2}-1} \bigg( 1 + \frac{m}{n}z\bigg)^{-\frac{m+n}{2}} \end{align}\]
となります。なお、書き方にバリエーションが色々あり、上記の式以外を紹介していることも多いです。
2 等分散性の検定
F分布の導出は二つのχ二乗分布からでした。何に使えば良く分からないわけですが、二つの分布の母分散\(\sigma^2\)が等しいという帰無仮説の下で、標本分散を\(s^2_x\)と\(s^2_y\)、χ二乗統計量を\(X\)と\(Y\)とおくと、
\[ z = \frac{X/m}{Y/n} = \frac{s^2_x/\sigma^2}{s^2_y/\sigma^2} = \frac{s^2_x}{s^2_y} \]
となるので、標本分散比の分布になっていることが分かります。
Rで実際に検定してみましょう。
と乱数をつくり
[1] 0.5087843教科書的にp値を出せます。
var.testを使う方が簡単です。
F test to compare two variances
data: x and y
F = 1.4575, num df = 9, denom df = 14, p-value = 0.5088
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.4541509 5.5355408
sample estimates:
ratio of variances
1.457507 実用上、等分散性の検定はANOVAやOLSなどで制約付きモデルと制約無しモデルの比較で用いることが多く、var.testを用いることは少ないと思います。
昔はStudentのt検定を行うか、Welchのt検定を行うかを、等分散性の検定をかけて判定するという悪習があったのですが、今は迷わずWelchのt検定をかけるほうが望ましいとされています。
また、等分散性の検定は正規分布を前提にしており、他の分布で検定をかけると大きなバイアスが入ることが知られています。観測値の真の分布は通常、分かりませんから、使うには強い仮定が必要です。
2.1 尖度による自由度補正
F検定が正規分布にしか適用ができないのは、分布の裾野の厚さ、尖度が問題であって、尖度が分かればそれで自由度を補正してより広い分布に使えることが知られています（O’Neill (2014)）。参考文献で示されている補正法を実装してみます。
kurtosis <- function(...){
# 尖度の不偏推定量を計算（注意：正規分布の尖度が0ではなく3になる方）
args <- list(...)
kappa <- numeric(length(args))
for(i in 1:length(args)){
a <- args[[i]]
n <- length(a)
m <- mean(a)
kappa[i] <- n * (n + 1) / (n - 1) * sum((a - m)^4) / sum((a - m)^2)^2
}
kappa
}
on2014ss2ss <- function(a, b, alternative = NULL){
# サブサンプルとサブサンプルの分散比の統計量を、自由度補正してF検定
n <- c(length(a), length(b))
s2 <- c(var(a), var(b))
kappa <- kurtosis(c(a - mean(a), b - mean(b)))
DF_n <- function(n) 2*n / (kappa - (n - 3)/(n - 1))
cpf <- function(i, j) pf(s2[i]/s2[j], DF_n(n[i]), DF_n(n[j]))
if(is.null(alternative)) alternative <- "two.sided"
(switch(alternative, "two.sided" = function(){
2*min(cpf(1, 2), cpf(2, 1))
}, "less" = function(){
cpf(1, 2)
}, "greater" = function(){
cpf(2, 1)
}))()
}実際にガンマ分布に応用してみましょう。
[1] 0.4629295これだと有用性が分からないので、教科書的なF検定、上で紹介したO’Neillの方法、（詳細は省きますが）Levene法の三つをシミュレーションで比較しました。
まず、5%に近ければ近いほどよい偽陽性率です。パラメーターが同じサンプルサイズ70と30の二つの群を、1000回比較しました。
| norm | laplace | unif | gamma | |
|---|---|---|---|---|
| F-test | 0.041 | 0.132 | 0.006 | 0.114 |
| O’Neill | 0.050 | 0.050 | 0.044 | 0.054 |
| levene | 0.043 | 0.046 | 0.043 | 0.044 |
F検定は正規分布（norm）以外では偽陽性率がよくないです。O’Neillとleveneは概ね設定した危険率通りの値になっています。
次に、偽陽性率が一定のとき、高ければ高いほどよい真陽性率です。母分散が異なるサンプルサイズ70と30の二つの群を、1000回比較しました。
| norm | laplace | unif | gamma | |
|---|---|---|---|---|
| F-test | 0.833 | 0.681 | 0.553 | 0.966 |
| O’Neill | 0.721 | 0.391 | 0.683 | 0.851 |
| levene | 0.661 | 0.440 | 0.449 | 0.895 |
上で紹介したO’Neillの方法が、levene法と遜色のない結果になっているのが分かります。
3 分散分析（ANOVA）
ANOVAはF検定の応用で最もよく使われているものです。何かの従属変数の説明において、オス/メスや品種などの因子ごとの影響を統制したときに、誤差が同じと言えるかを検定します。異なる場合は、因子が従属変数に影響していることがわかります。
オスとメスのような2つの水準の因子であればt検定をかけることもできますが、品種のように3以上になりうる場合はANOVAを使うことになります。また、因子の主効果をみる一元配置分散分析（one-way ANOVA）だけではなく、因子と因子の交互作用を見る二元配置分散分析（two-way ANOVA）を行うことができます。
ただし、教科書的なANOVAを用いなくなっている分野も多いです。ANOVAは説明変数を因子としたOLSと同等です。OLSの方は因子以外の説明変数も同時に入れることができ、制約付きモデルと制約無しモデルのANOVAを手軽にかけることができるためです。OLSを使ったANOVAは、共分散分析（ANCOVA）と呼ばれます。
3.1 一元配置分散分析（one-way ANOVA）
複数の因子を考えても同様の計算が成り立ちますし、二元配置も交互作用を表す因子を追加するだけなので、一元配置分散分析をしっかり理解することが肝要です。
3.1.1 推定モデル
因子に\(k\)種類の水準/群があるとします。因子の水準/群\(g\)の\(i\)番目の観測値\(Y_{gi}\)が、平均\(\mu\)、水準/群ごとの効果\(\tau_g\)、誤差項\(\epsilon_{gi}\)で表されるとします。
\[ Y_{gi} = \mu + \tau_g + \epsilon_{gi} \]
水準ごとの効果の合計は\(0\)とします。合計を定めないと\(\mu\)があるので一意に定まりません。
\[ \sum^k_{g=0} \tau_g = 0 \]
統計的仮説検定をかけるときの帰無仮説は、すべての\(\tau_g\)が\(0\)です。
3.1.2 平方和の分解
観測値から平均値をひいて二乗した数の和を、平方和といいます。左辺と右辺の各項ごとに平方和を考えます。
\[\begin{align} \mathit{TSS} &= \sum^k_{g=1} \sum^{n_g}_{i=1} (Y_{gi} - \bar{Y})^2 \\ \mathit{SST} &= \sum^k_{g=1} \sum^{n_g}_{i=1} (\bar{Y_{g}} - \bar{Y})^2 = \sum^k_{g=1} n_g (\bar{Y_{g}} - \bar{Y})^2 \\ \mathit{SSE} &= \sum^k_{g=1} \sum^{n_g}_{i=1} (Y_{gi} - \bar{Y_{g}})^2 \end{align}\]
\(\bar{Y}\)は全体の平均値、\(n_g\)は水準ごとのサンプルサイズ、\(\bar{Y}_g\)は水準ごとの平均値です。
\(\mathit{TSS}\)は全体の平方和、\(\mathit{SST}\)は因子効果の平方和、\(\mathit{SSE}\)は誤差項の平方和になります。
このとき全体の平方和を、因子効果の平方和と誤差項の平方和に分解することができます。
\[ \mathit{TSS} = \mathit{SST} + \mathit{SSE} \]
こうなることを確認しましょう。
\[\begin{align} \mathit{TSS} &= \sum^k_{g=1} \sum^{n_g}_{i=1} (Y_{gi} - \bar{Y})^2 \\ &= \sum^k_{g=1} \sum^{n_g}_{i=1} (Y_{ij} - \bar{Y}_g + \bar{Y}_g - \bar{Y})^2 \\ &= \sum^k_{g=1} \sum^{n_g}_{i=1} \big[ (Y_{ij} - \bar{Y}_g)^2 + 2(Y_{ij} - \bar{Y}_g)(\bar{Y}_g - \bar{Y}) + (\bar{Y}_g - \bar{Y})^2 \big] \\ &= \sum^k_{g=1} \bigg[ \sum^{n_g}_{i=1} (Y_{ij} - \bar{Y}_g)^2 + 2 (\bar{Y}_g - \bar{Y}) \sum^{n_g}_{i=1} (Y_{ij} - \bar{Y}_g) + \sum^{n_g}_{i=1} (\bar{Y}_g - \bar{Y})^2 \bigg] \end{align}\]
\(\sum^{n_g}_{i=1} (Y_{ij} - \bar{Y}_g) = n_g \bar{Y}_g - n_g \bar{Y}_g = 0\)に注意すると、
\[\begin{align} \mathit{TSS} &= \sum^k_{g=1} \sum^{n_g}_{i=1} (Y_{ij} - \bar{Y}_g)^2 + \sum^k_{g=1} \sum^{n_g}_{i=1} (\bar{Y}_g - \bar{Y})^2 \\ &= \mathit{SSE} + \mathit{SST} \end{align}\]
3.1.3 因子効果の平方和の期待値
\(E[\mathit{SST}]\)の計算の前に準備をしましょう。
\[\begin{align} \bar{Y}_g &= \frac{1}{n_g} \sum^{n_g}_{i=1} Y_{gi} \\ &= \frac{1}{n_g} \sum^{n_g}_{i=1} (\mu + \tau_g + \epsilon_{gi})\\ &= \mu + \tau_g + \bar{\epsilon}_g \quad \mbox{where} \ \ \bar{\epsilon}_g = \frac{1}{n_g} \sum^{n_g}_{i=1} \epsilon_{gi} \end{align}\]
\(\epsilon_{gi}\)はi.i.d.な確率変数で、\(E\big[ \epsilon_{gi} \big] = 0\)、\(\mathit{VAR}\big[ \epsilon_{gi} \big] = \sigma^2\)なので、
\[\begin{align} E\big[ \bar{\epsilon}_{g} \big] &= 0 \\ \mathit{VAR}\big[ \bar{\epsilon}_{g} \big] &= \frac{\sigma^2}{n} \quad \mbox{where} \ \ n = \sum^k_{g=1} n_g \end{align}\]
になります。
同様に
\[\begin{align} \bar{Y} &= \frac{1}{n} \sum^k_{g=1} \sum^{n_g}_{i=1} Y_{gi} \\ &= \frac{1}{n} \sum^k_{g=1} \sum^{n_g}_{i=1} (\mu + \tau_g + \epsilon_{gi})\\ &= \mu + \bar{\tau} + \bar{\epsilon} \quad \mbox{where} \ \ \bar{\tau} = \frac{1}{n} \sum^k_{g=1} n_g \tau_g, \ \bar{\epsilon} = \frac{1}{n} \sum^k_{g=1} \sum^{n_g}_{i=1} \epsilon_{gi} \end{align}\]
になります。なお、
\[\begin{align} \bar{\tau} &= \frac{1}{n} \sum^k_{g=1} n_g \tau_g \\ \bar{\epsilon} &= \frac{1}{n} \sum^k_{g=1} \sum^{n_g}_{i=1} \epsilon_{gi} \end{align}\]
です。\(\tau_g\)は定数なので\(\bar{\tau}\)も定数になり、
\[\begin{align} E\big[ \bar{\epsilon} \big] &= 0 \\ \mathit{VAR}\big[ \bar{\epsilon} \big] &= \frac{\sigma^2}{n} \end{align}\]
となります。
因子効果の平方和の期待値を計算していきます。
\[\begin{align} E[\mathit{SST}] &= E\bigg[ \sum^k_{g=1} n_g (\bar{Y}_g - \bar{Y})\bigg] \\ &= E\bigg[ \sum^k_{g=1} n_g (\tau_g + \bar{\epsilon}_g - \bar{\tau} - \bar{\epsilon}) \bigg] \\ &= E\bigg[ \sum^k_{g=1} n_g (\tau_g - \bar{\tau})^2 + \sum^k_{g=1} 2n_g(\tau_g - \bar{\tau})(\bar{\epsilon}_g - \bar{\epsilon}) + \sum^k_{g=1} n_g(\bar{\epsilon}_g - \bar{\epsilon})^2 \bigg]\\ &= E\bigg[ \sum^k_{g=1} n_g (\tau_g - \bar{\tau})^2 - \bar{\epsilon}) + \sum^k_{g=1} n_g(\bar{\epsilon}_g - \bar{\epsilon})^2 \bigg] \end{align}\]
ここで
\[\begin{align} E[\sum^k_{g=1} n_g(\bar{\epsilon}_g - \bar{\epsilon})^2] &= E\big[ \sum^k_{g=1} (n_g \bar{\epsilon}_g^2 - 2n_g\bar{\epsilon}_g\bar{\epsilon} + n_g\bar{\epsilon}^2) \big]\\ &= E\big[ \sum^k_{g=1} n_g \bar{\epsilon}_g^2 - 2n_g\bar{\epsilon}^2 + n\bar{\epsilon}^2 \big]\\ &= E\big[\sum^k_{g=1} n_g \bar{\epsilon}_g^2 - n_g\bar{\epsilon}^2 \big] \\ &= \sum^k_{g=1} n_g E[\bar{\epsilon}_g^2] - n_gE[\bar{\epsilon}^2 ] \\ &= k\sigma^2 - \sigma^2 \\ &= (k-1)\sigma^2 \end{align}\]
なので、
\[ E[\mathit{SST}] = \sum^k_{g=1} n_g (\tau_g - \bar{\tau})^2 + (k - 1)\sigma^2 \]
となります。
3.1.4 誤差項の平方和の期待値
\(\mathit{SSE}\)は級数和が二重になっているのですが、内側の級数和の期待値はt検定の説明での不偏分散の導出のときと同様に
\[\begin{align} E[ \mathit{SSE} ] &= E\bigg[ \sum^k_{g=1} \sum^{n_g}_{i=1} (Y_{gi} - \hat{Y}_g)^2 \bigg] \\ &= \sum^k_{g=1} E\bigg[\sum^{n_g}_{i=1} (Y_{gi} - \hat{Y}_g)^2 \bigg] \\ &= \sum^k_{g=1} (n_g - 1) \sigma^2 \\ &= (n - k)\sigma^2 \end{align}\]
と計算できます。自由度が\(n-1\)ではなく、\(n-k\)になるのに注意してください。
3.1.5 検定統計量とその意味
ANOVAの検定統計量としてのF値は以下のようになります。
\[ F = \frac{\mathit{SST}/(k-1)}{\mathit{SSE}/(n-k)} = \frac{\mathit{MST}}{\mathit{MSE}} \]
因子効果の平均平方\(\mathit{MST}\)となる分子の期待値は
\[ \frac{E[\mathit{SST}]}{k-1} = E\bigg[ \frac{1}{k-1}\sum^k_{g=1} n_g (\tau_g - \bar{\tau})^2 \bigg] + \sigma^2 \]
なので、帰無仮説\(H_0: \tau_1 = \cdots = \tau_k = 0\)の下で、\(\sigma^2\)の不偏推定量となります。\(H_0\)では右辺第一項が\(0\)になるからです。自由度は\(k-1\)です。
誤差項の平均平方\(\mathit{MSE}\)となる分母は、分散\(\sigma^2\)の不偏推定量となります。
帰無仮説の下では、分子と分母は分散\(\sigma^2\)の不偏推定量となり、この検定統計量に対してF検定を用いることができることがわかります。
3.1.6 Rによる実践
まずは教科書的に検定してみましょう。irisデータセットを使います。
y <- iris$Sepal.Length
g <- iris$Species
n <- length(y)
k <- length(levels(g))
TSS <- sum((y - mean(y))^2)
mean_y_by_g <- tapply(y, g, mean)[g]
SSE <- sum((y - mean_y_by_g)^2)
# SST <- TSS - SSE と計算もできる
SST <- sum((mean_y_by_g - mean(y))^2)
df_g <- k - 1
df_e <- n - k
(f_value <- (SST/df_g)/(SSE/df_e))[1] 119.2645[1] 3.339338e-31anova関数とaov関数を組み合わせると、簡単に検定できます。
Analysis of Variance Table
Response: Sepal.Length
Df Sum Sq Mean Sq F value Pr(>F)
Species 2 63.212 31.606 119.26 < 2.2e-16 ***
Residuals 147 38.956 0.265
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1なお、表示のDfは自由度、Sum Sqは平方和、Mean Sqは平均平方和です。
3.1.6.1 群間比較
ANOVAで因子全体が影響しているとは言えるわけですが、因子のどの水準/群とどの水準/群に差異があるか分かりません。
aovの結果オブジェクトをTukeyHSD関数に入れると、水準と水準の差の信頼区間とp値の計算を多重比較補正つきでしてくれます。
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = Sepal.Length ~ Species, data = iris)
$Species
diff lwr upr p adj
versicolor-setosa 0.930 0.6862273 1.1737727 0
virginica-setosa 1.582 1.3382273 1.8257727 0
virginica-versicolor 0.652 0.4082273 0.8957727 0群間比較はガブリエル比較区間による視覚化などの選択肢もあるので、状況にあわせて利用しましょう。
3.1.6.2 OLS
ここまでの記述を超える方法ですが、OLSを使って推定することもできます。
mf <- model.frame(Sepal.Length ~ Species, iris)
X <- model.matrix(terms(mf), mf)
y <- model.response(mf)
r_lm_0 <- lm(Sepal.Length ~ 1, iris)
r_lm_1 <- lm(Sepal.Length ~ Species, iris)
anova(r_lm_1, r_lm_0)Analysis of Variance Table
Model 1: Sepal.Length ~ Species
Model 2: Sepal.Length ~ 1
Res.Df RSS Df Sum of Sq F Pr(>F)
1 147 38.956
2 149 102.168 -2 -63.212 119.26 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1p値の表記方法に差異はありますが、どれもF値は同じ値になりますね。
3.2 二元配置分散分析（two-way ANOVA）
複数の因子による一元配置分散分析と、それら因子の交互作用の一元配置分散分析を組み合わせたものです。 性別と種の因子があるパルマーペンギンのデータセットで試してみましょう。
次のパッケージを付け加えます: 'palmerpenguins'以下のオブジェクトは 'package:datasets' からマスクされています:
penguins, penguins_rawAnalysis of Variance Table
Response: bill_length_mm
Df Sum Sq Mean Sq F value Pr(>F)
species 2 7015.4 3507.7 654.1894 <2e-16 ***
sex 1 1135.7 1135.7 211.8066 <2e-16 ***
species:sex 2 24.5 12.2 2.2841 0.1035
Residuals 327 1753.3 5.4
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 13.2.1 プロット
二元配置分散分析の場合、交互作用をどう図示するかと言う問題があります。よくあるのが、
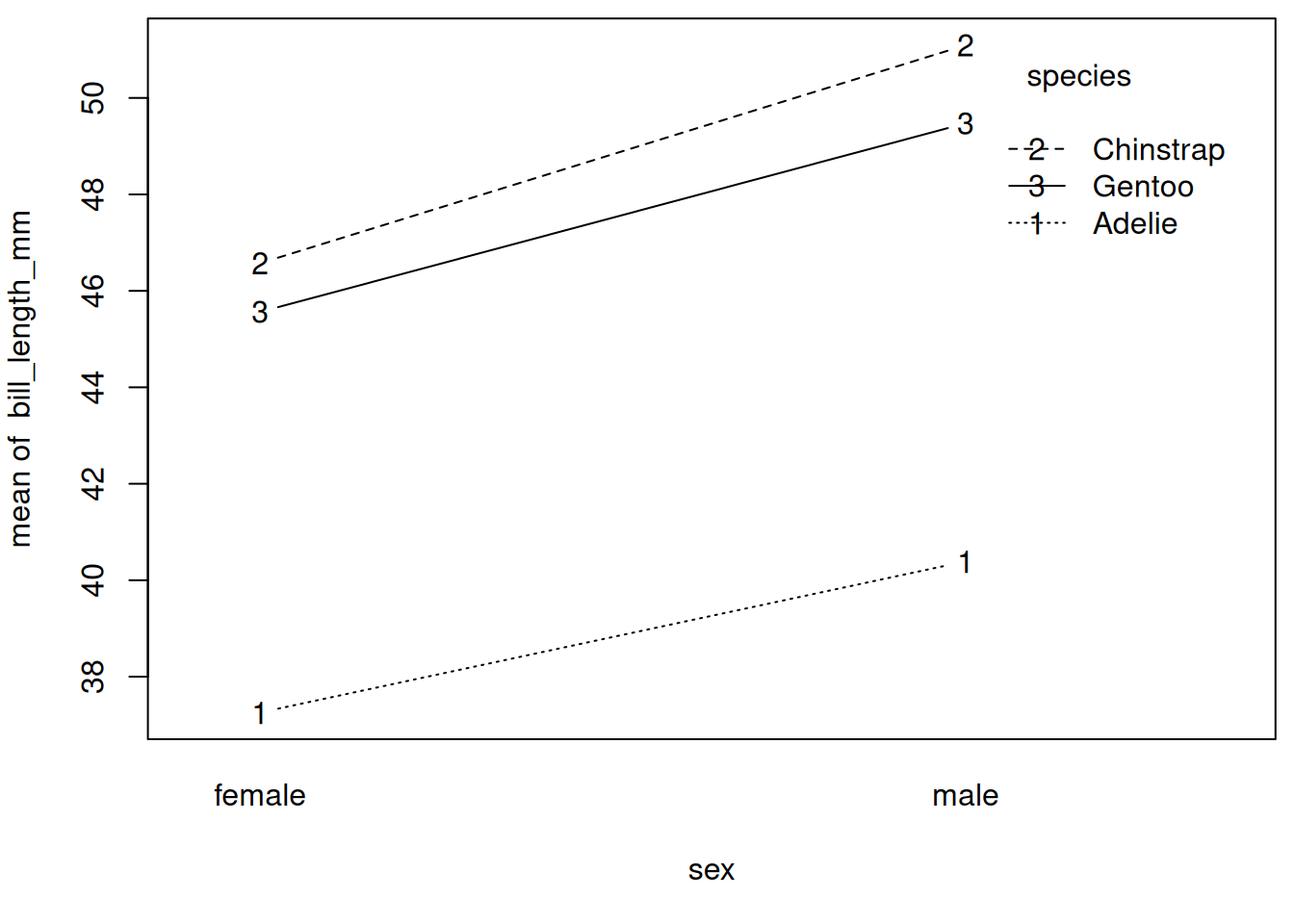
と言う風に、横軸に一方の因子をとり、他方の因子ごとに線を引く方法です。因子と因子の間に中間点はないので奇妙に思われるかも知れませんが、因子ごとの線が並行でない場合は交互作用があることになります。
ggplot2だとggpubr::gglineで同様のプロットが出せ、さらに標準誤差なども簡単に描き込んでくれます。
3.3 高度な手法
ANOVAには、既に紹介したANCOVAの他、クラスカル＝ウォリス一元配置分散分析といったノンパラメトリック手法の代替や、応答変数が複数の多変量分散分析（MANOVA）、ANCOVAを多変量に拡張したMANCOVAといった発展的な手法があります。MANOVA/MANCOVAは社会科学分野では見かけない気がしますが、心理学やその応用のマーケティング分野では一般的なようです。