t検定は、標本の平均値がゼロなどの特定の値から、もしくは、二標本の平均値の差が、誤差と言えないほど離れているかを判定する代表的な手続きで、統計解析で広く使われています。t分布の導出を確認して、その理屈を抑えましょう。
1 グラム=シュミットの正規直交化
学部一般教養の線形代数の教科書にも載っているグラム=シュミットの正規直交化(orthonormalization)を思いしましょう。
まず、任意の\(n\)本の線形独立なベクトル\(\{\nu_i\}_{i \in \{ j \in \mathbb{N} \mid 1 \le j \le n \}}\)を、\(n\)本の直交ベクトル\(\{\mu_i\}_{i \in \{ j \in \mathbb{N} \mid 1 \le j \le n \}}\)に変換します。
大仰な感じがしますが、実際はベクトル\(x\)と\(y\)の内積を\((x, y)\)と置いて、
\[\begin{align} \mu_1 &= \nu_1 \\ \mu_2 &= \nu_2 - \frac{(\mu_1, \nu_2)}{(\mu_1, \mu_1)} \mu_1\\ \mu_3 &= \nu_3 - \frac{(\mu_1, \nu_3)}{(\mu_1, \mu_1)} \mu_1 - \frac{(\mu_2, \nu_3)}{(\mu_2, \mu_2)} \mu_2\\ &\vdots\\ \mu_i &= \nu_i - \frac{(\mu_1, \nu_i)}{(\mu_1, \mu_1)} \mu_1 - \frac{(\mu_2, \nu_3)}{(\mu_2, \mu_2)} \mu_2 - \cdots - \frac{(\mu_{i-1}, \nu_3)}{(\mu_{i-1}, \mu_{i-1})} \mu_{i-1} \\ &\vdots\\ \mu_n &= \nu_n - \sum^{n-1}_{j=1} \frac{(\mu_j, \nu_n)}{(\mu_j, \mu_j)} \mu_j \end{align}\]
と計算するだけです。\(\nu_i\)から\(\{\mu_j\}_{1 \le j \le i-1}\)とその大きさで表される成分を抜いて、\(\mu_i\)としています。
何をしているかと言うと、ベクトルは他のベクトルで成分分解することができるわけですが、\(\{\mu_j\}_{1 \le j \le i-1}\)と直交しない成分を消してしまうことで、\(\{\mu_j\}_{1 \le j \le i-1}\)と直交する成分だけを残しています。\(\mu_i\)は\(\{\mu_j\}_{1 \le j \le i-1}\)と直交するように計算され、\(\{\mu_j\}_{i+1 \le j \le n}\)は\(\mu_i\)と直交するように計算されるので、\(\{\mu_i\}_{i \in \{ j \in \mathbb{N} \mid 1 \le j \le n \}}\)に含まれるベクトルはそれぞれ直交することになります。
次に、直交ベクトルを内積が\(1\)になるように正規化します。
\[ \tilde{\mu_i} = \frac{\mu_i}{\sqrt{(\mu_i, \mu_i)}} \]
これで正規直交化したベクトルの族\(\{\tilde{\mu_i}\}_{i \in \{ j \in \mathbb{N} \mid 1 \le j \le n \}}\)ができました。
1.1 ある形式の線形独立なベクトルの正規直交化
各行が線形独立なベクトルとなっている、以下のような行列を考えます。
\[ V = \begin{pmatrix} \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \cdots & \frac{1}{\sqrt{n}} \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \]
これをグラム=シュミットの正規直交化すると、\(1\)行目の各成分は\(\frac{1}{\sqrt{n}}\)と不変になります。
\[ \tilde{\mu_1} = \frac{1}{\sqrt{n}} \bigg/ \frac{1}{\sqrt{\sum^n_{j=1} \frac{1}{\sqrt{n}} \frac{1}{\sqrt{n}} }} = \frac{1}{\sqrt{n}} \]
Rのコードで確認しておきましょう。
gsp <- function(n = 4, V = { V <- diag(n); V[1, ] <- rep(1/sqrt(n), n); V }){
U <- matrix(NA, n, n)
U[1, ] <- V[1, ]
for(j in 2:n){
W <- sapply(1:(j-1), \(i){
c(t(V[j, ]) %*% U[i, ] / (t(U[i, ]) %*% U[i, ])) * U[i, ]
})
U[j, ] <- V[j, ] - apply(W, 1, sum)
}
N <- t(sapply(1:n, \(i){
U[i, ]/sqrt(c(t(U[i, ])%*%U[i, ]))
}))
# U: orthogonalization
# N: orthonormalization
list(o = U, on = N)
}
# 5行5列を計算してみる
round(gsp(5)$on, 5) [,1] [,2] [,3] [,4] [,5]
[1,] 0.44721 0.44721 0.44721 0.44721 0.44721
[2,] -0.22361 0.89443 -0.22361 -0.22361 -0.22361
[3,] -0.28868 0.00000 0.86603 -0.28868 -0.28868
[4,] -0.40825 0.00000 0.00000 0.81650 -0.40825
[5,] -0.70711 0.00000 0.00000 0.00000 0.70711\(1/\sqrt{5}\)は、約0.44721です。
正規直交化したベクトルでつくられた行列の逆行列は、転置行列になり、直交行列の条件を満たします。転置した行列の行\(i\)と、もとの行列の列\(j\)の内積は、\(i=j\)のとき\(1\)であり、\(i\ne j\)のとき\(0\)だからです。
2 標本平均と不偏分散
\(\{X_i\}_{i \in \{ j \in \mathbb{N} \mid 1 \le j \le n \}}\)を正規分布\(\mathcal{N}(\mu, \sigma^2)\)に従う確率変数の標本とします。標本平均は
\[\begin{align} \bar{X} &= \frac{1}{n}\sum^n_{i=1} X_i \end{align}\]
となります。
標本分散を母分散の推定量として扱うと過小推定バイアスが入るので、小標本ではとくに不偏分散を用います。不偏分散は、確率変数の分散と、標本平均の分散を分けて計算することで導出できます。
\[\begin{align} &E\bigg[\sum^n_{i=1} ( X_i - \bar{X} )^2 \bigg] \\ &= E\bigg[\sum^n_{i=1} ( X_i - \mu + \mu - \bar{X} )^2 \bigg] \\ &= E\bigg[\sum^n_{i=1} (X_i - \mu)^2 - n(\bar{X} - \mu)^2 \bigg] \\ &= n\sigma^2 - E\bigg[n(\bar{X} - \mu)^2 \bigg] \end{align}\]
となりますが、\(E[(\bar{X} - \mu)^2]\)は\((x_1 + x_2 + x_3 + \cdots + x_n)/n\)の分散なので、
\[\begin{align} &\mathit{VAR}\bigg(\frac{x_1 + x_2 + x_3 + \cdots + x_n}{n}\bigg) \\ &=\frac{\mathit{VAR}(x_1 + x_2 + x_3 + \cdots + x_n)}{n^2} \\ &=\frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n} \end{align}\]
となることに注意すると、
\[ E\bigg[\sum^n_{i=1} ( X_i - \bar{X} )^2 \bigg] = n\sigma^2 - \sigma^2 = (n-1)\sigma^2 \]
なので、
\[ \sigma^2 = E\bigg[\frac{\sum^n_{i=1} ( X_i - \bar{X} )^2}{n-1} \bigg] \]
となります。よって不偏分散は、
\[\begin{align} s^2 &= \frac{1}{n-1}\sum^n_{i=1} (X_i - \bar{X})^2 \end{align}\]
です。
3 不偏分散が従う分布の導出
必要なのは不偏分散が従う分布なのですが、ほとんど同じ計算なので標本平均と不偏分散が独立であることの証明を確認します。
標準化された観測値のベクトル\(U\)を考えます。
\[\begin{align} U = \begin{pmatrix} \frac{X_1 - \mu}{\sigma} \\ \vdots \\ \frac{X_n - \mu}{\sigma} \end{pmatrix} \end{align}\]
\(U\)に1行目が\(1/\sqrt{n}\)の直交行列\(A\)をかけた行列を\(V\)と置きます。そのような\(A\)がとれることは、前節で確認しました。
\[ V = \begin{pmatrix} V_1 \\ \vdots \\ V_n \end{pmatrix} = AU \]
正規化直交行列の逆行列が転置行列になることに注意して、\(V\)と\(U\)の関係を確認しましょう。
\[ \sum^n_{i=1}V_i^2 = {}^t\!VV = {}^t\!(AU)(AU) = {}^t\!U({}^t\!AA)U = {}^t\!UU = \sum^n_{i=1}U_i^2 \]
\(\bar{X}\)と\(s^2\)を書き直します。
\[\begin{align} \bar{X} &= \frac{1}{n}\sum^n_{i=1} X_i \\ &= \frac{1}{n}\sum^n_{i=1} (\mu + \sigma U_i) \\ &= \mu + \frac{\sigma}{\sqrt{n}} \sum^n_{i=1} \frac{U_i}{\sqrt{n}} \\ &= \mu + \frac{\sigma}{\sqrt{n}} \sum^n_{i=1} A_{1i} U_i \\ &= \mu + \frac{\sigma}{\sqrt{n}} V_1 \end{align}\]
\[\begin{align} s^2 &= \frac{1}{n-1}\sum^n_{i=1}(X_i - \bar{X})^2 \\ &= \frac{1}{n-1}\sum^n_{i=1}(\mu + \sigma U_i - \mu - \sigma \bar{U})^2 \quad \bigg( \bar{U} = \sum^n_{i=1} \frac{U_i}{n} \bigg)\\ &= \frac{\sigma}{n-1}\sum^n_{i=1}(U_i - \bar{U})^2 \\ &= \frac{\sigma}{n-1}\sum^n_{i=1}(U_i^2 - 2 U_i \bar{U} + \bar{U}^2) \\ &= \frac{\sigma}{n-1} \big( \sum^n_{i=1} U_i^2 - 2 \sum^n_{i=1} U_i \bar{U} + \sum^n_{i=1} \bar{U}^2 \big) \\ &= \frac{\sigma}{n-1} \big( \sum^n_{i=1} U_i^2 - 2 n \bar{U} \bar{U} + n \bar{U}^2 \big) \\ &= \frac{\sigma}{n-1} \big( \sum^n_{i=1} U_i^2 - n \bar{U}^2 \big) \\ &= \frac{\sigma}{n-1} \bigg( \sum^n_{i=1} U_i^2 - \bigg( \frac{ n \bar{U}}{ \sqrt{n} } \bigg)^2 \bigg) \\ &= \frac{\sigma}{n-1} \bigg( \sum^n_{i=1} U_i^2 - \bigg( \frac{ \sum^n_{i=1} U_i }{ \sqrt{n} } \bigg)^2 \bigg) \\ &= \frac{\sigma}{n-1} \big( \sum^n_{i=1} U_i^2 - \big( \sum^n_{i=1} A_{1i} U_i \big)^2 \big) \\ &= \frac{\sigma}{n-1} \big( \sum^n_{i=1} V_i^2 - V_1^2 \big) \\ &= \frac{\sigma}{n-1} \sum^n_{i=2} V_i^2 \end{align}\]
\(V_1\)と\(\{V_i\}_{2\le i \le n}\)の式になりました。
ところで確率変数を要素にとる\(n\)次元ベクトル\(V\)が\(D\)の中に入る確率と、\(U\)が\(A^{-1}D\)の中に入る確率は同じになります。\(U\)の各要素が標準正規分布に従い、対称行列の行列式が\(\pm 1\)であることに注意すると、
\[\begin{align} P(V \in D) &= P(U \in A^{-1}D) \\ &= \int_{A^{-1}D} \frac{1}{\sqrt{2\pi}} \exp(-\frac{u_1^2}{2}) \cdots \frac{1}{\sqrt{2\pi}} \exp(-\frac{u_n^2}{2}) du_1 \cdots du_n \\ &= \int_{A^{-1}D} \bigg( \frac{1}{\sqrt{2\pi}} \bigg)^n \exp(-\frac{\sum^n_{i=1} u_i^2}{2}) du_1 \cdots du_n \\ &= \int_{D} \bigg( \frac{1}{\sqrt{2\pi}} \bigg)^n \exp(-\frac{\sum^n_{i=1} v_i^2}{2}) \mid A \mid dv_1 \cdots dv_n \\ &= \int_{D} \bigg( \frac{1}{\sqrt{2\pi}} \bigg)^n \exp(-\frac{\sum^n_{i=1} v_i^2}{2}) dv_1 \cdots dv_n \\ &= \int_{D} \frac{1}{\sqrt{2\pi}} \exp(-\frac{v_1^2}{2}) \cdots \frac{1}{\sqrt{2\pi}} \exp(-\frac{v_n^2}{2}) dv_1 \cdots dv_n \end{align}\]
と\(V\)の各要素も標準正規分布に従う確率密度になることが分かります。よって、\(V\)の要素と要素は独立です。これで、\(V_1\)と\(\{V_i\}_{2\le i \le n}\)が独立になることが分かりました。
さらに
\[ s^2\frac{n-1}{\sigma} = \sum^n_{i=2} V_i^2 \]
は、標準正規分布に従う\(n-1\)個の確率変数の二乗和なので、自由度\(n-1\)のχ二乗分布1に従うことが分かります。
4 t分布の導出
母集団の平均\(\mu\)と標準誤差\(\sigma\)が分かっていれば、標本平均を標準化した値
\[ Z = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \]
が、標準正規分布に従います。\(\mu\)を\(\bar{X}\)で、\(\sigma\)を\(s\)で置き換えて、Z値を計算し、標準正規分布を用いてp値を計算すると、Z検定になります。しかし、小サンプルの場合、不偏分散の誤差を考慮しないZ検定は誤差が大きくなります。
そこで、
\[ T = \frac{\bar{X} - \mu}{s/\sqrt{n}} = \frac{\bar{X} - \mu}{\sqrt{s^2/n}} \]
の分布を求めて統計的仮説検定を行います。t検定です。
\(\bar{X}\)は標準正規分布に従います。\(s^2\)は自由度\(n-1\)のχ二乗分布に従うことは前節で確認しました。標準正規分布とχ二乗分布の同時確率密度を考えれば、\(t<\alpha\)となる確率を求めることができます。
\(u=\bar{X} - \mu\), \(v=s^2\), \(k=n-1\)と置いて、
\[ P(T<\alpha) = \int_{\frac{u}{\sqrt{v/n}} < \alpha} \bigg( \frac{1}{\sqrt{2\pi}} \exp\bigg(-\frac{u^2}{2}\bigg)\bigg) \bigg( \frac{1}{\Gamma(k/2) 2^{k/2}} v^{k/2 - 1} \exp\bigg(-\frac{v}{2}\bigg)\bigg) dudv \]
\(t=u/\sqrt{v/k}\), \(v=v\)で変数変換します。
\[ P(T<\alpha) = \int_{-\infty}^\alpha \int_0^\infty \frac{1}{\sqrt{2\pi}2^{k/2}\Gamma(k/2)} \exp\bigg(-\frac{ut^2}{2k}-\frac{v}{2}\bigg)v^{k/2-1} \begin{vmatrix} \sqrt{v/k} & \frac{-2k}{u}\big(\frac{v}{k}\big)^\frac{3}{2} \\ 0 & 1 \end{vmatrix} dv dt \]
\(q=vt^2/(2k)+v/2\), \(t=t\)で変数変換します。
\[\begin{align} &P(T<\alpha) \\ &= \int_{-\infty}^\alpha \int_0^\infty \frac{1}{\sqrt{2\pi}2^{k/2}\Gamma(k/2)} \exp(-q)\bigg( \frac{q}{t^2/(2k) + 1/2} \bigg)^{k/2-1} \begin{vmatrix} \frac{1}{t^2/(2k) + 1/2} & \frac{k}{\nu t} \\ 0 & 1 \end{vmatrix} dq dt\\ &= \int_{-\infty}^\alpha \int_0^\infty \frac{1}{\sqrt{k\pi}2^{(k+1)/2}\Gamma(k/2)} q^{\frac{k+1}{2}-1} \exp(-q) \frac{1}{\big( t^2/(2k) + 1/2 \big)^{k/2+1}} dq dt\\ &= \frac{\Gamma\big(\frac{k+1}{2}\big)}{\sqrt{k\pi}\Gamma\big(\frac{k}{2}\big)} \int_{-\infty}^\alpha \bigg( \frac{t^2}{k} + 1 \bigg)^{-\frac{k+1}{2}}dt \end{align}\]
自由度\(k\)のt分布の累積分布関数が導出できました。確率密度関数は微分積分学の基本公式から、
\[ f(t) = \frac{\Gamma\big(\frac{k+1}{2}\big)}{\sqrt{k\pi}\Gamma\big(\frac{k}{2}\big)} \bigg( \frac{t^2}{k} + 1 \bigg)^{-\frac{k+1}{2}} \]
となります。
5 標本平均の検定
効果ゼロなどの帰無仮説が正しいときに、分析したデータから計算したパラメーターの推定量と同じかより極端な推定量が観察される相対頻度であるp値を求めましょう。
標本平均が特定の値であると言う帰無仮説に対するp値は、t分布の累積分布関数からそのまま出ます。実際に試してみましょう。
データセットをつくります。
生成されたサンプルを教科書的に推定すると、次のようになります。
s <- sd(x)
m <- mean(x)
n <- length(x)
H0 <- 0 # 帰無仮説
T <- (m - H0)/sqrt(s^2/n)
sprintf("左片側 p値: %.5f", (p.value <- pt(T, n - 1)))[1] "左片側 p値: 0.96559"[1] "右片側 p値: 0.03441"[1] "両側 p値: 0.06883"ptはt分布の累積分布関数になります。
図示すると、
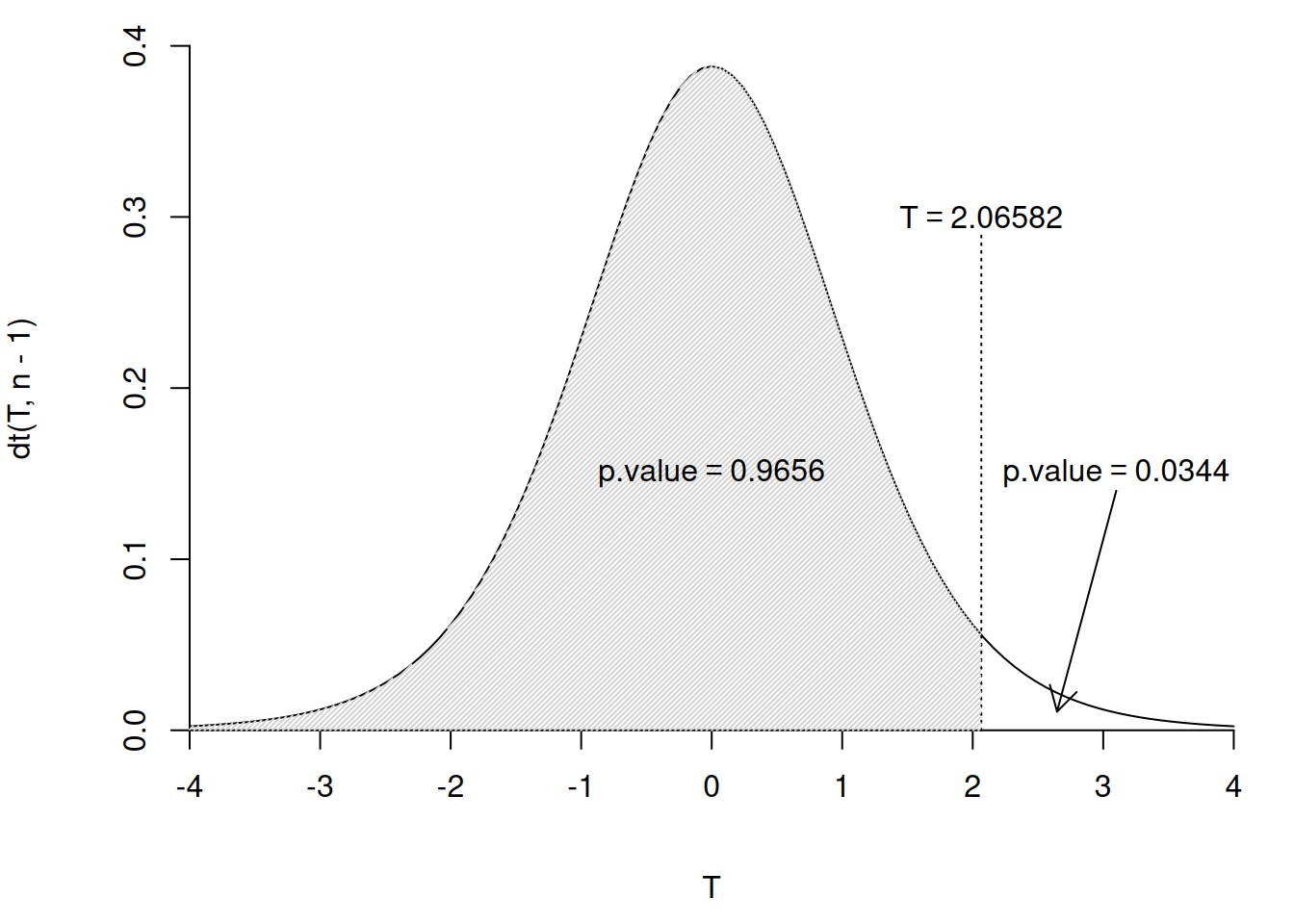
t分布をT統計量で分断し、左側と右側の積分値を求めていることが分かりやすいと思います。
左側の灰色の領域は、帰無仮説(と不偏分散)が真だとして、同じサンプルサイズの観測を繰り返したときに、観測値された値と同じか、より小さい値が得られる確率で、右側の白い領域は、同じか、より大きい値が得られる確率です。両側検定のp値は小さい方のp値の2倍となります。それぞれの側の有意水準は表示の半分で評価するため、p値を2倍にしないと有意水準の値そのままと比較できないためです。
便利なt.test関数があるので、こんなに書かなくても大丈夫です。
One Sample t-test
data: x
t = 2.0658, df = 9, p-value = 0.06883
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.05163488 1.13823318
sample estimates:
mean of x
0.5432992 6 二標本の平均値の差の検定
統制変数が入れられないので理工系の研究室のラボでないとあまり使わない気もしますが、仕組みは抑えておきましょう。
6.1 Student’s t-test
教科書には載っているのですが、二標本が等分散という強い仮定が置かれていて、かつ、現在ではその仮定を外した分析を手軽に利用できるため、実用上は使うべきではなくなったStudent’s t testを説明します。実用には使えませんが、後述するWelch’s t testの説明の前提知識になるので理屈は把握しておきましょう。
同じ分布の母集団から無作為抽出された二つの標本があるとします。それぞれの標本に含まれる観測値は、独立で同一の分布に従います。この二標本の平均値\(\bar{X}_1\)と\(\bar{X}_2\)の差の分布を考えましょう。
だいたいの場合、\(\bar{X}_1\)と\(\bar{X}_2\)はそれぞれ正規分布に従うと看做せます。中心極限定理があるからです。また、二標本に含まれる個々の観測値の分散\(\sigma^2\)は同一ですから、以下のように書けます。
\[\begin{align} \bar{X}_1 &\sim \mathcal{N}(\mu, \frac{\sigma^2}{n_1})\\ \bar{X}_2 &\sim \mathcal{N}(\mu, \frac{\sigma^2}{n_2}) \end{align}\]
サンプルサイズを\(n_1\)と\(n_2\)とおくと、二標本の差の分布は
\[ \bar{X}_1 - \bar{X}_2 \sim \mathcal{N}(0, \frac{\sigma^2}{n_1} + \frac{\sigma^2}{n_2}) \]
になります。
\(\sigma^2\)は観察不能なため、不偏分散\(s_1\)と\(s_2\)を代わりに使うことを考えます。
自由度を\(k_1\),\(k_2\)と置き、\(k_1s_1 + k_2s_2\)の分布を考えましょう。\(k_1s_1\)と\(k_2s_2\)は、これまで見てきたようにχ二乗分布に従います。\(k_1=n_1-1\),\(k_1=n_1-2\)であることも確認してきました。
さて、χ二乗分布には再生性があります。自由度\(k\)のときのモーメント母関数が
\[ M_X^k(t) = (1-2t)^{-\frac{k}{2}} \]
になるからです2。それぞれχ二乗分布に従う変数の合計のモーメント母関数は
\[ M_X^{k_1}(t)M_X^{k_2}(t) = (1-2t)^{-\frac{k_1+k_2}{2}} \]
となり、やはりχ二乗分布のモーメント母関数になっています。
\(s^2(n-1)/\sigma = \sum^n_{i=2}V_i^2\)であったことに注意すると、
\[ \frac{s_1^2(n_1-1)}{\sigma^2} + \frac{s_2^2(n_2-1)}{\sigma^2} \]
は、自由度\(n_1 + n_2 - 2\)のχ二乗分布に従います。
また、平均値の差の(プールされた)不偏分散\(s_p\)は
\[ s_p^2 = \frac{s_1^2(n_1-1) + s_2^2(n_2-1)}{n_1 + n_2 - 2} \]
と書けます。\(s(n-1)\)が\(\sigma\sum^n_{i=2}V_i^2 \sim \chi^2_{n-1}\)であったことをに注意すると、\(s_1^2(n_1-1) + s_2^2(n_2-1)\)は\(n_1 + n_2 - 2\)個の標準正規分布に従う変数の二乗和だからです。
サンプルの抽出方法の前提から\(E[s_1]=E[s_2]\)を仮定できるので、検定統計量
\[ T = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{ s_p^2 \big( \frac{1}{n_1} + \frac{1}{n_2} \big) }} \]
が自由度\(n_1 + n_2 - 2\)のt分布に従うことが分かります。
6.2 Welch’s t-test
観測値の分散がすべて等しいというのは、かなり強い仮定です。男女のような属性ごとで分散が異なるのはよくあることですし、ランダム化比較実験であっても、処置によって介入群と処置群の性質が変わってしまうかも知れません。
幸い、等分散の仮定を緩める手法Welch’s t testがあり、広く使われています。この方法はt検定に用いる自由度を変えて補正します。等分散であった場合はStudent’s t testと同様の結果になるので、迷わずWelch’s t testを使いましょう3。
ウェルチのt検定で用いる自由度の計算方法を確認しましょう。まず、
\[\begin{align} V_s &= \sum^n_{n=2} V_i^2 \\ \sigma^2_p &= \bigg(\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\bigg) \\ W &= \frac{k s_p^2}{\sigma_p^2} \\ Y &= \frac{\bar{X}_1 - \bar{X}_2}{\sigma_p} \end{align}\]
と定義します。
\(s^2 = \sigma^2 \sum^n_{n=2} V_i^2 / k\)であったわけで、等分散であれば\(W = V_s\)です。また、\(Y/\sqrt{V_s/k}\)はt分布になります。
\(\sigma_1 \ne \sigma_2\)のときに、\(k\)を調整して、\(Y/\sqrt{W/k}\)を\(Y/\sqrt{V_s/k}\)で近似できないか考えます。具体的には\(W\)と\(V_s\)の一次、二次モーメントが一致するように\(k\)を定めます。
まず、一次モーメントを考えましょう。
\(sigma_p^2\)の定義に注意すると、
\[ E[W] = \frac{k}{\sigma_p^2} \bigg(\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\bigg) = k \]
となります。
一方、\(V_s\)はχ二乗分布に従うので、
\[ E[V_s] = k \]
となります。
一次モーメントは\(k\)に関わらず一致します。
次に、二次モーメントを考えます。
\[ E[W^2] = E[V_s^2] \iff \mathit{VAR}(W) = \mathit{VAR}(V_s) \]
なので、分散を考えます。
\[ \mathit{VAR}(W) = \sqrt{k^2}{\sigma_p^4} \bigg( \frac{\mathit{VAR}(s_1^2)}{n_1^2} + \frac{\mathit{VAR}(s_2^2)}{n_2^2} \bigg) \]
ここで
\[ \frac{(n_1-1)s^2}{\sigma_1^2} \sim \chi^2_{n_1 - 1} \]
なので、\(\frac{(n_1-1)s^2}{\sigma_1^2}\)はχ二乗分布の分散と等しくなります。よって、
\[\begin{align} \frac{(n_1 - 1)^2 \mathit{VAR}(s_1^2)}{\sigma_1^4} &= 2(n_1 - 1) \\ \mathit{VAR}(s_1^2) &= \frac{2\sigma_1^4}{n_1 - 1} \end{align}\]
同様に
\[ \mathit{VAR}(s_2^2) = \frac{2\sigma_2^4}{n_2 - 1} \]
よって
\[ \mathit{VAR}(W) = \frac{k^2}{\sigma_p^4} \bigg( \frac{2\sigma_1^4}{n_1^2(n_1 - 1)} + \frac{2\sigma_2^4}{n_2^2(n_2 - 1)} \bigg) \]
となります。
一方、\(V_s\)はχ二乗分布に従うので
\[ \mathit{VAR}(V_s) = 2k \]
です。
よって、\(\mathit{VAR}(W) = \mathit{VAR}(V_s)\)となるのは、
\[ k = \frac{ \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} }{ \frac{1}{n_1 - 1}\big( \frac{\sigma_1^2}{n_1} \big)^2 + \frac{1}{n_2 - 1}\big( \frac{\sigma_2^2}{n_2} \big)^2 } \]
のときになります。実際には\(\sigma_1\)と\(\sigma_2\)は観察できないので、実際の自由度は\(s_1\)と\(s_2\)を代わりに使って計算します。これがWelch-Satterwaithe approximationです。
Rのt.test関数は、二標本の平均値の差の検定においては、標準でWelch’s
t testを用います。
Welch Two Sample t-test
data: x1 and x2
t = 0.38559, df = 9.945, p-value = 0.7079
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.6643788 0.9421981
sample estimates:
mean of x mean of y
0.6926676 0.5537579 dfに小数点がありますね。実際のところ、あれこれ考える必要はありません。
6.3 対応のある検定(paired t test)
二標本の差の検定なのですが、二つのベクトルの対応する値と値を引いて一つのベクトルにしてから検定をかけるので、手法としては帰無仮説がゼロの一標本の平均値の検定になります。
set.seed(710)
x1 <- rnorm(10, mean = 1, sd = 1.5)
x2 <- runif(10, min = 0, max = 1)
t.test(x1, x2, paired = TRUE)
Paired t-test
data: x1 and x2
t = 0.14945, df = 9, p-value = 0.8845
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-0.7055616 0.8053790
sample estimates:
mean difference
0.04990873
One Sample t-test
data: x1 - x2
t = 0.14945, df = 9, p-value = 0.8845
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.7055616 0.8053790
sample estimates:
mean of x
0.04990873 χ二乗分布の導出はRによる適合度のχ二乗検定を参照してください。↩︎
χ二乗分布はガンマ関数の特殊形になります。ガンマ関数のモーメント母関数の導出を参考にしてください。↩︎
等分散性の検定でStudentとWelchのどちらにするかを選択した場合、それに対するp値の補正が必要になりますが、一般的な手法として確立していません。↩︎
