1 ロジットモデルとは？
二項分布もしくは多項分布の確率質量関数の中の確率をロジスティック関数で表したモデルを、ロジットモデルと呼びます。例えば試行回数\(m\)、生起回数\(n\)の二項分布の確率質量関数は
\[ f_X(n) = {}_m\!C_n p^{n}(1-p)^{m-n} \]
と生起確率\(p\)を使って表されますが、ここで
\[ p = \frac{e^y}{1 + e^y} \]
と、\(p\)をロジスティック関数で表します。\(y\)を\(p\)に写すことを、逆ロジット変換と言います。\(y\)は実数で、値域が\((-\infty, +\infty)\)の線形関数で説明されることが一般的です。
値粋が\((0, 1)\)の単調増加関数であればロジスティック関数である必要はなく、例えば正規分布の累積分布関数を用いるプロビット分析もありますが、ロジスティック関数は数理的に取り扱いやすいため、ロジットモデルが標準的な分析ツールになっています1。
1.1 効用関数からの導出
ロジットモデルは、経済学の意思決定の文脈で基礎付けることもできます。教科書2の内容を確認していきましょう。
選択肢\(j\)を選んだときの効用関数\(U\)を以下のように定義しましょう。
\[ U_{j} = V_{j} + \epsilon_{j} \]
\(V_{j}\)は観測可能な説明変数に応じた効用で、\(\epsilon_{j}\)は観測不能なガンベル分布（Gumbel distribution）に従う誤差項です。ガンベル分布は、ある標本サイズの確率変数の最大値を正規化した分布が、標本サイズを増やしたときに漸近する分布です3。
選択肢\(i\)を選択肢\(j\)より選好する確率を考えます。
\[ \begin{align} P(U_{i} > U_{j}) &= P(V_{i} + \epsilon_{i} > V_{j} + \epsilon_{j}) \\ &= P(\epsilon_{j} < \epsilon_{i} + V_{i} - V_{j}) \end{align} \]
\(\epsilon_{i}\)が所与の定数とすると、ガンベル分布の累積分布関数なので
\[ P(U_{i} > U_{j}) = \exp(-\exp(-(\epsilon_{i} + V_{i} - V_{j}))) \]
と表すことができます。
選択肢\(i\)が選ばれる確率を考えます。他の選択肢すべてと効用を比較して、選択肢\(i\)からの効用が大きいことになるので、すべての選択肢と比較した同時確率密度になります。
\[ P(U_{i}) = \prod_{i \ne j} P(U_{i} > U_{j}) \]
\(\epsilon_{i}\)は実際には確率変数なので、ガンベル分布の累積分布関数と確率密度関数を用いて積分します。
\[\begin{align} P(U_{i}) &= \int_{-\infty}^\infty \bigg( \prod_{i \ne j} \exp(-\exp(-(\epsilon_{i} + V_{i} - V_{j}))) \bigg ) \\ &\quad \exp(-\epsilon_{i}) \exp(-\exp(-\epsilon_{i})) d \epsilon_{i} \end{align}\]
\(i=j\)のとき\(\epsilon_{i} + V_{i} - V_{j} = \epsilon_{i}\)なので、確率密度関数の部分を級数部分に融合できます。
\[ P(U_{i}) = \int_{-\infty}^\infty \bigg( \prod \exp(-\exp(-(\epsilon_{i} + V_{i} - V_{j}))) \bigg ) \exp(-\epsilon_{i}) d \epsilon_{i} \]
指数の外側の積を、指数の中の和に書き換えます。
\[ P(U_{i}) = \int_{-\infty}^\infty \exp(\sum -\exp(-(\epsilon_{i} + V_{i} - V_{j})))) \exp(-\epsilon_{i}) d \epsilon_{i} \]
後の計算のために式を整理します。
\[ P(U_{i}) = \int_{-\infty}^\infty \exp(\sum - \exp(\epsilon_{i}) \exp(-(V_{i} - V_{j})))) \exp(-\epsilon_{i}) d \epsilon_{i} \]
ここで積分の基底を取り替えます。つまり、\(\exp(-\epsilon_{i})\)を\(t\)に置換します。\(d\epsilon_{i} = dt/t\)になり、\((-\infty, \infty)\)の区間が\((0, \infty)\)になるので、
\[ P(U_{i}) = \int^0_\infty t \exp(-t \sum - \exp(\epsilon_{i})) -\frac{dt}{t} \]
\(t\)について整理し、積分区間を逆にしてマイナスを消します。
\[ P(U_{i}) = \int^\infty_0 \exp(-t \sum - \exp(\epsilon_{i})) dt \]
あとは複合関数の積分の問題で、
\[ P(U_{i}) = \frac{1}{\sum \exp(-(V_i - V_j))} = \frac{\exp(V_i)}{\sum \exp(V_j)} \]
が導出できます。さらに、\(V_i = V_j\)のとき\(\exp(-(V_i - V_i)) = 1\)になることに注意すると、中央から
\[ P(U_{i}) = \frac{1}{1 + \sum_{i \ne j} \exp(-(V_i - V_j))} \]
よく見かける形状のロジスティック関数が導出できます。\(V_i\)や\(V_j\)は一意に定まりませんが、\(V_i-V_j\)は一意になるので推定が容易になります。
ガンベル分布を用いる明確な理由は不明です。数理的に扱いやすい4からだと思いますが。
2 二項選択モデル（binominal）
冒頭で紹介したものです。非線形モデルになるので教科書的には最尤法で推定しますが、Rでは一般化線形モデル（GLM）5を推定するglm関数で推定するのが一般的です。
2.1 GLMによる推定
実際に推定してみましょう。
# データセットをダウンロードして、二項選択モデルをGLMで推定
summary(r_glm <- glm(r ~ x1 + x2, (df01 <- read.table("https://wh.anlyznews.com/R/dataset/for_logit.txt", sep = "\t", header = TRUE)), family = binomial()))
Call:
glm(formula = r ~ x1 + x2, family = binomial(), data = (df01 <- read.table("https://wh.anlyznews.com/R/dataset/for_logit.txt",
sep = "\t", header = TRUE)))
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.3125 0.3759 0.831 0.406
x1 0.7171 0.1667 4.301 1.70e-05 ***
x2 0.7610 0.1578 4.823 1.41e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 137.989 on 99 degrees of freedom
Residual deviance: 52.623 on 97 degrees of freedom
AIC: 58.623
Number of Fisher Scoring iterations: 6モデル式とデータフレームの指摘はlmと同様で、family = binomial()のところが異なり、ここでロジット関数による二項選択モデルのリンク関数を指定しています。
戻り値のオブジェクトは。lmのそれと同様に扱えます。信頼区間はconfint(r_glm)で出ます。係数と標準誤差を抜き出したい場合はcoef(summary(r_glm))です。
ロジットモデルをプロットすることは稀です。線形部分の観測値（のロジット変換）は\(\infty\)もしくは\(-\infty\)になるため、プロットできません。線形部分の予測値を逆ロジット変換したものと観測値はプロットすることができるので見てみましょう。
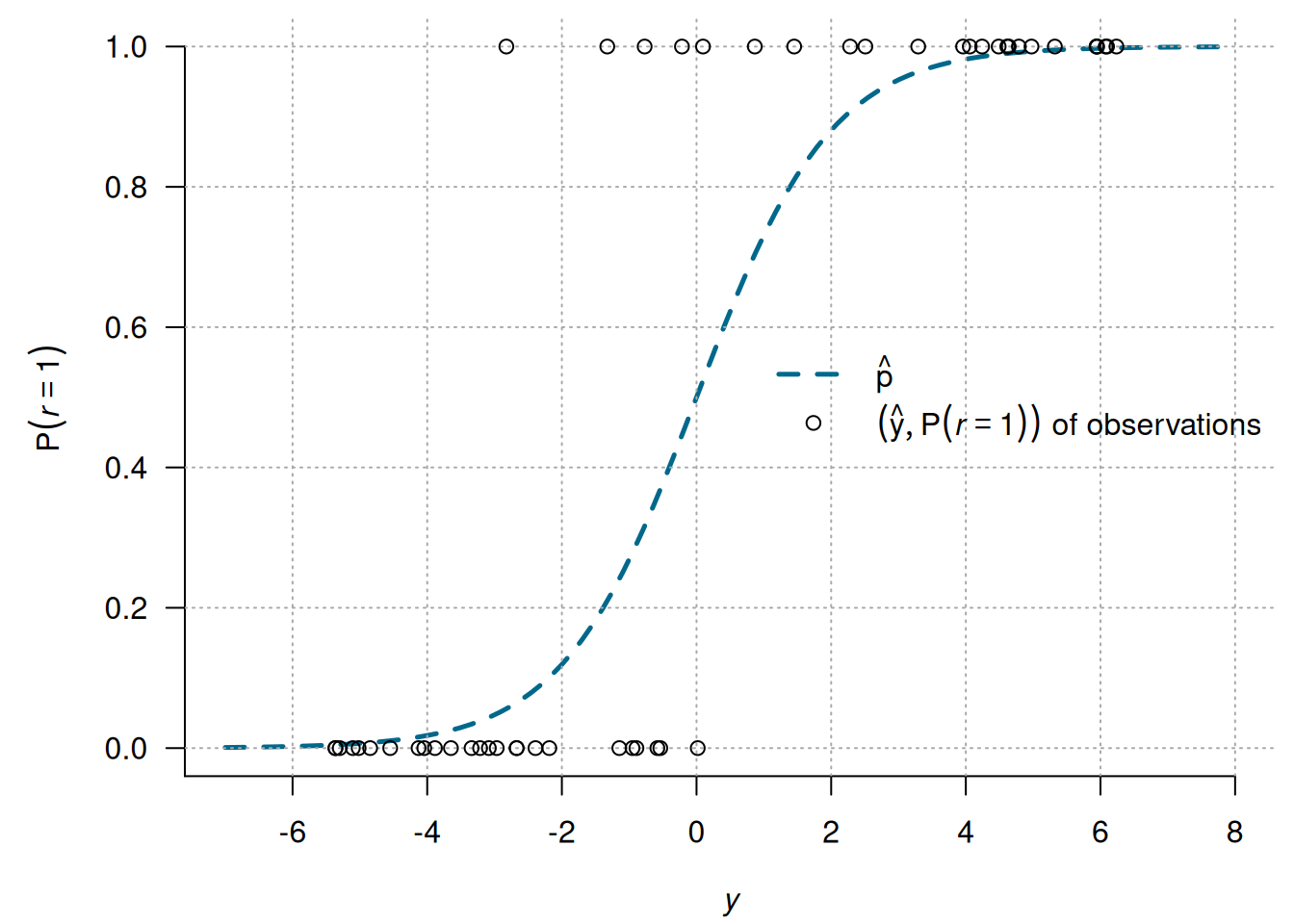
2.1.1 予測値
ロジットモデルの予測値は、線形部分の予測値と生起確率の予測値の2種類があります。
newdata <- data.frame(x1 = 1, x2 = 2) # 予測する説明変数の値
predict(r_glm, newdata) # 線形部分の予測値; type = "link" 1
2.551694 1
0.9276872 type = "terms"で予測値の各項（\(\beta_i
x_i\)）が出てきたりもしますが、上の2つを覚えておけば十分でしょう。
2.1.2 限界効果
ロジットモデルは非線形なので、説明変数を増やしたときに予測値がどの程度増えるのかという限界効果が説明変数の値によって変わり、係数から把握するのが困難です。限界効果を計算します。
限界効果は微分量なので、解析的に一階微分を導出して変数に値を代入してもよいですし、微細な値\(h\)で説明変数を\(\pm h\)して予測値\(\hat{p}_{+h}\)と\(\hat{p}_{-h}\)を出して、\((\hat{p}_{+h}-\hat{p}_{-h})/h/2\)をする数値解析の手法でも計算できます。どちらも難しくはないです。しかし、説明変数が多いと手間隙がかかるのでパッケージを用いましょう。
図示する場合はeffectsパッケージが使いやすいです。
library(effects)
r_pe <- predictorEffects(r_glm, ~ x1 + x2, confidence.level = 0.99)
plot(r_pe, axes = list(grid = TRUE), ticks = list(at = c(0.01, 0.1, 0.5, 0.9, 0.99)))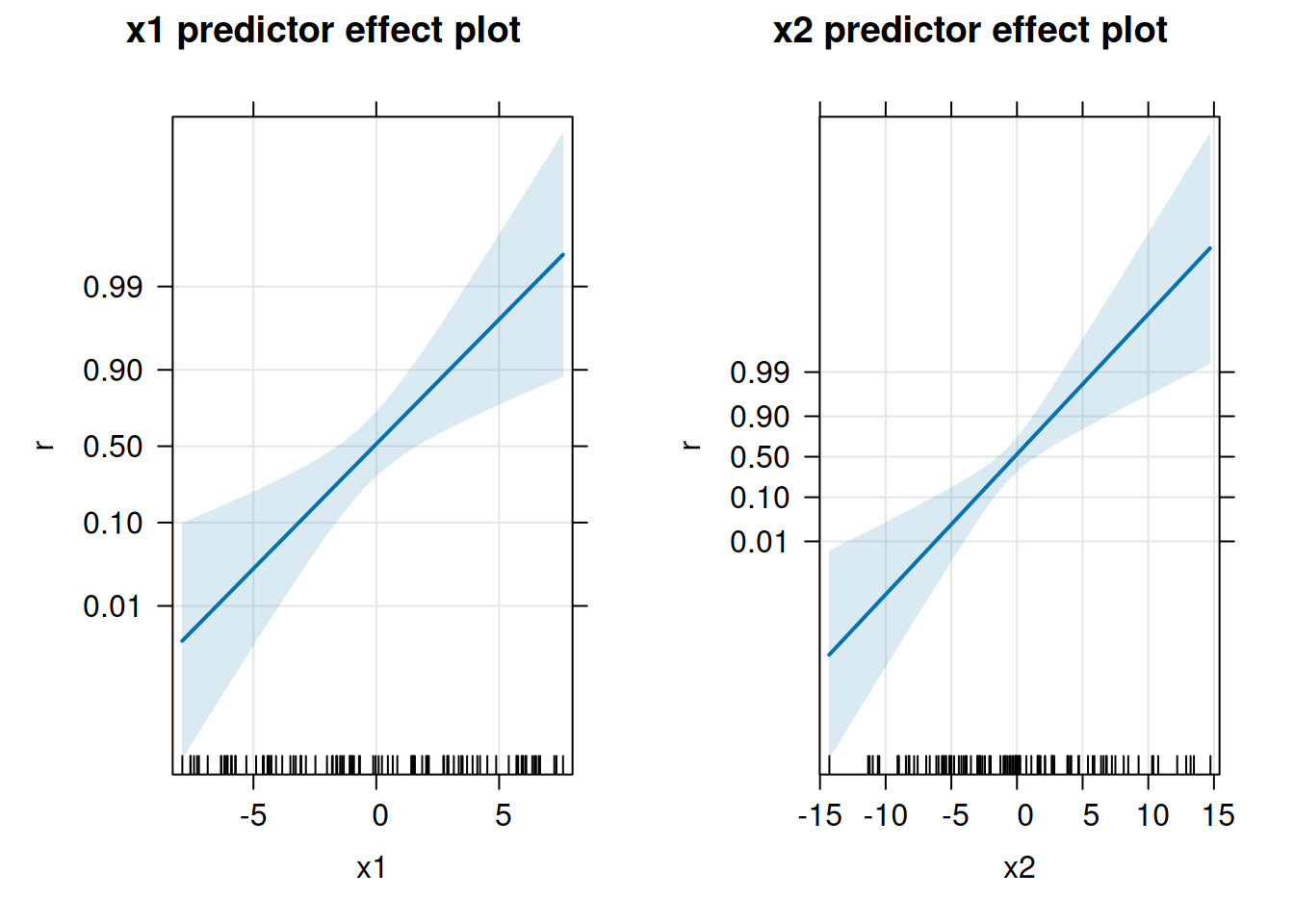
プロットの横軸ではない他の変数は、平均値が仮定されています。
この例のように図を見ても傾向が分かりづらいときは、全体の傾向をあらわす数字で限界効果を確認します。この用途ではmarginaleffectsが有用です。
library(marginaleffects)
# 引用してくださいメッセージを消す（謝辞などで言及してあげましょう）
options(marginaleffects_startup_message = FALSE)
# 平均値をまとめてデータフレームにする
(dfm <- as.data.frame(apply(df01, 2, mean, simplify = FALSE))) r x1 x2
1 0.46 -0.2495172 -0.3276298
Term Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
x1 0.179 0.0418 4.28 <0.001 15.7 0.0968 0.261
x2 0.190 0.0400 4.75 <0.001 18.9 0.1113 0.268
Type: response
Comparison: dY/dX観測値すべての限界効果の平均である平均限界効果を見ることが多いですが、それも簡単に計算できます。
Term Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
x1 0.0581 0.00659 8.82 <0.001 59.6 0.0452 0.0710
x2 0.0617 0.00295 20.86 <0.001 318.7 0.0559 0.0674
Type: response
Comparison: dY/dX2.2 最尤法による推定
（対数）尤度関数を書けば、optimなどの最適化アルゴリズムを用いて推定することもできます。
mf <- model.frame(r ~ x1 + x2, df01) # モデル式とデータフレームをまとめる
X <- model.matrix(terms(mf), mf) # 説明変数を行列にまとめる
r <- model.response(mf) # 被説明変数を取り出す
objf <- function(theta){ # 目的関数
y <- X %*% theta
p <- 1/(1 + exp(-y))
# 各行のCombination項は1!/(1!0!)=1になる
sum(r*log(p) + (1 - r)*log(1 - p))
}
# optimは目的関数を最小化しようとするので、controlで目的関数の符号の反転を指示
(r_optim <- optim(c(0, 0, 0), objf, method = "L-BFGS-B", control = list(fnscale = -1)))$par
[1] 0.3125301 0.7171431 0.7610165
$value
[1] -26.31164
$counts
function gradient
17 17
$convergence
[1] 0
$message
[1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"ほぼ同じ推定結果が得られます。
ただし、指数を使うので桁あふれしやすいため上述の素朴なコードだと推定できない場合が多く、素朴な場合でもglmを使う場合よりもだいぶ手間隙がかかっています。区間推定や予測値や限界効果の計算などを考えると、手間隙の差はもっと大きくなります。glmを使っておきましょう。
3 多項選択モデル（multinominal logit）
効用関数から多項ロジットモデルを導出しました。線形部分で加算でつながれている項の構造に種類があります。
日本の戸籍は家系図と言うよりは、誰が誰の戸主かを記した書類です。第二次世界大戦が終わった後、戸主の権限はなくなったので、もはや意味の無い情報を管理していると言えます。
基本的な多項ロジットモデルでは、選択時の状況（choice situation）を示す変数と、選択（alternative）によって変わる係数で線形部分が構成されます。個体の性別など、説明変数の値が選択肢から独立したものである一方、選択肢にあたえる影響が異なる場合に用いられます。
選択肢が\(J\)種類あるとすると、それから\(1\)を引いた\(J-1\)本の方程式を推定します。確率の和が\(1\)になるため、\(J\)本だと冗長だからです。よって、説明変数がひとつ増えると、推定する係数は\(J-1\)増えることになります。
3.1 条件付ロジット（conditional logit）
財やサービスの価格や品質のような、選択肢の特徴の影響に関心がある場合もあります。その場合は、選択肢によって値が変わる説明変数と共通の係数の項を線形部分に加えます。社会科学の方言ではこれをconditional logitと呼びます6。
説明変数は選択時の状況と独立とは限りません。利用する交通機関を考えた場合、利用者によって移動元も移動先も異なりますから、目的地までの所用時間は選択肢（alternative）だけではなく、選択時の状況（choice situation）でも変化します。
選択肢が\(J\)種類あるとすると、それから\(1\)を引いた\(J-1\)本の方程式を推定しますが、係数は共通になるので説明変数が1つ増えたときに推定する係数は同じく1つ増えることになります。
3.2 混合ロジット（mixed logit）
線形部分が、選択時の状況（choice situation）を示す説明変数と選択（alternative）によって変わる係数の項と、選択（alternative）によって変わる説明変数と共通の係数の項で構成されるモデルを、混合ロジットと混乱を招く呼び名7で呼ぶときがあります。
\(y\)が線形予測値、\(p\)が生起確率の予測値、\(i\)が個体、\(J\)が選択肢の数、\(c\)が選択されたとする選択肢、\(K_c\)が条件付変数の数、\(K_n\)が条件なし変数の数、\(z\)が条件付変数、\(x\)が条件なし変数、\(\beta\)が推定される係数で、\(I_{c=j}\)は\(c\)と\(j\)が一致するとき\(1\)になる単純関数です。
\[\begin{align} p_{i,c} &= \frac{ \exp(y_{i,c} - y_{i,J}) }{1 + \sum_{j=1}^{J-1} \exp(y_{i,j-1} - y_{i,J})} \\ y_{i,c} &= \sum_{k=1}^{K_c} \sum_{j=1}^{J} I_{c=j} \alpha_k z_{i,J(k-1)+j} + \sum_{j=1}^{J} I_{c=j} \sum_{k=1}^{K_n} \beta_{K_n(j - 1) + k} x_{i,k} \end{align}\]
一見、複雑そうですが、（対数）尤度関数を書けばoptimなどを使い最適化アルゴリズムで（桁があふれやすいのですが）推定できます。なお尤度関数は、各行の観測数は\(1\)なので、個体\(i\)が実際に選択した選択肢を\(c_i\)と置いて、\(\prod^n_{i=1} p_{i,c_i}\)となります。
以上に加えて、選択（alternative）によって変わる説明変数と選択（alternative）によって変わる係数の項が加えられることがあります。車と電車で目的地までの所要時間が変わる影響があるが、同じ時間でも電車の方がよりストレスになる場合などに使います8。このタイプの項の変数を\(w\)、係数を\(\gamma\)、項の数を\(K_w\)とすると以下のように書けます。
\[\begin{align} y_{i,c} &= \sum_{k=1}^{K_c} \sum_{j=1}^{J} I_{c=j} \alpha_k z_{i,J(k-1)+j} + \sum_{j=1}^{J} I_{c=j} \sum_{k=1}^{K_n} \beta_{K_n(j - 1) + k} x_{i,k} + \sum_{j=1}^{J} I_{c=j} \sum_{k=1}^{K_w} \gamma_{K_w(j - 1) + k} w_{i,k} \\ \end{align}\]
実用ではmlogitパッケージを用いるのが一般的です。mlogitはvignietteにコード例が充実している9のですが、そこにある利用例をひとつ紹介します。
library(mlogit)
library("zoo")
data("Fishing", package = "mlogit")
# データを整形してmlogitが処理できる形式にする
Fish <- mlogit.data(Fishing, varying = c(2:9), shape = "wide", choice = "mode")
# mlogitで推定を行う．モデル式は
# 1. choice situation and alternative specificな説明変数とalternative specificな係数（省略するには0を入れる）
# 2. choice situation specificな説明変数とalternative specificな係数（省略するには0を入れる; (3)が無ければ省略可）
# 3. choice situation and alternative specificな説明変数とchoice situation and alternative specificな係数（省略可）
# を | でつなぐ。
(m <- mlogit(mode ~ price | income | catch, data = Fish))
Call:
mlogit(formula = mode ~ price | income | catch, data = Fish, method = "nr")
Coefficients:
(Intercept):boat (Intercept):charter (Intercept):pier
8.4184e-01 2.1549e+00 1.0430e+00
price income:boat income:charter
-2.5281e-02 5.5428e-05 -7.2337e-05
income:pier catch:beach catch:boat
-1.3550e-04 3.1177e+00 2.5425e+00
catch:charter catch:pier
7.5949e-01 2.8512e+00 # 説明変数の平均値を求める
z <- with(Fish, data.frame(price = tapply(price, idx(m, 2), mean), catch = tapply(catch, idx(m, 2), mean), income = mean(income)))
# 平均値における限界効果を計算
# typeはaもしくはrの2文字を指定（デフォルトはaa）
# aは絶対値，rは相対値．1番目の文字は確率，2番目は変数での指定になる
effects(m, covariate = "income", type = "aa", data = z) beach boat charter pier
1.132964e-06 3.113069e-05 -2.408677e-05 -8.176876e-06 モデル選択のための統計的仮説検定は、waldtest，lmtest，scoretestで、ワルド検定、尤度比検定、ラグランジェ乗数検定を行えます。
なお、mlogitでも限界代替効果と消費者余剰は係数と説明変数の値から計算しないといけないようです。
3.3 入れ籠ロジット（nested logit）
ロジットモデルにはIIAと呼ばれる数理的な性質があります。\(a\)を選択する確率と\(b\)を選択する確率のオッズ比を計算してみましょう。
\[ \frac{p_a}{p_b} = \frac{\exp(y_a - y_J)/\sum_{i=1}^{J-1} \exp(y_i - y_J)}{\exp(y_b - y_J)/\sum_{i=1}^{J-1} \exp(y_i - y_J)} = \exp(y_a - y_b) \]
他にどのような選択肢があるかは関係がないことが分かります。
バニラ味のアイスクリームと塩バター風味のポップコーンの二択に、チョコ味のアイスクリームが加わることを考えます。IIAなので、バニラ味のアイスクリームと塩バター風味のポップコーンが選ばれる確率の比は、チョコ味のアイスクリームが選択肢にあるかないかで代わりません。バニラ味のアイスクリームと塩バター風味のポップコーンの需要が同じ割合で減ることになります。また、バニラ味のアイスクリームの味が落ちたとき、塩バター風味のポップコーンとチョコ味のアイスクリームの需要が同じように増えます（交差弾性値が一定）。
このIIAという性質は、非直感的で、非現実的です。アイスクリームの種類が増えたとき、需要が大きく減るのは他のアイスクリームであって、ポップコーンでは無さそうですよね。種類が増えると選ぶ楽しみが増えて、ポップコーンの方が大きく影響を受けるのかも知れませんが、少なくとも需要の減少が一定と言うことは無さそうです。将来予測や反実仮想を考えるときに問題になりえます。
入れ籠ロジットモデルは、このIIAの性質を緩和することができます。アイスクリームとポップコーンの選択のロジットモデルと、アイスクリームの中でバニラ味とチョコ味の選択のロジットモデルの二つを同時に推定することで、選択肢の増減の影響を変化させます。多項プロビットモデルを使っても解決するのですが、IIAが問題になるときは入れ籠ロジットがよく使われています。
これもmlogitパッケージで推定できます。
4 集計データのオッズに対する推定
集計データから比率しか分からないときがありますが、オッズの対数をとると線形モデルになるので、比率しか分からなくても観測値に0%がなければ推定できます。
\[\begin{align} log(\frac{p_c}{p_J}) &= y_c - y_J \end{align}\]
二項ロジットの場合はOLSで、
\[ log(\frac{p_1}{p_0}) = \begin{pmatrix} Z_1 - Z_0 & X \end{pmatrix}\begin{pmatrix} \alpha \\ \beta_{1} - \beta_{0} \end{pmatrix} + \eta \]
を、多項ロジットのときはSUR10で
\[ \begin{pmatrix} log(\frac{p_1}{p_J}) \\ log(\frac{p_2}{p_J}) \\ \vdots \\ log(\frac{p_{J-1}}{p_J}) \end{pmatrix} = \begin{pmatrix} Z_1 - Z_J & X & O & \cdots & O \\ Z_2 - Z_J & O & X & \cdots & O \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ Z_{J-1} - Z_J & O & \cdots & \cdots & X \end{pmatrix}\begin{pmatrix} \alpha \\ \beta_{1} - \beta_{J} \\ \beta_{2} - \beta_{J} \\ \vdots \\ \beta_{J-1} - \beta_{J} \end{pmatrix} + \begin{pmatrix} \eta_1 \\ \eta_2 \\ \vdots \\ \eta_{J-1} \end{pmatrix} \]
と\(J-1\)本同時に回帰します。\(O\)は\(X\)と同じ大きさのゼロ行列です。\(\frac{p_j}{p_J}\)，\(\alpha\)，\(\beta_j\)，\(\eta_j\)（\(1 \leq j \leq J-1\)）はn次元ベクトルです。所謂conditionalな説明変数\(Z\)は、選択された選択肢のときの値をJ番目の選択肢のときの値で引いています。非conditionalな説明変数の係数は差分になります。
なお、オッズの信頼区間の計算で用いたりしますが、誤差項\(\eta\)の分布は漸近的に正規分布に従うことが知られています。OLSを使うことができますし、信頼区間を求めることも可能です。
4.1 予測確率
予測値がオッズではなくて確率で欲しいときは、\(i\)が\(1\)から\(J-1\)までの\(\log(p_i/p_J)\)の予測値\(\log(\widehat{p_i/p_J})\)を出した後、
\[ p_c = \frac{\exp(\log(\widehat{p_c/p_J}))}{1 + \sum_{j=1}^{J-1} \exp(\log(\widehat{p_j/p_J}))} \]
の右辺に値を代入して計算すれば、\(c\)を選択したときの確率\(p_c\)が出ます。
4.2 限界効果
\(\log(\widehat{p_c/p_J}) = (Z_c-Z_J)\alpha + X(\beta_c - \beta_J)\)であることに注意して、\(p_c\)を\(Z\)や\(X\)の要素で微分して値を代入して計算するか、説明変数を微小な値\(h\)で\(\pm h\)して予測値\(\hat{p}_{c,+h}\)と\(\hat{p}_{c,-h}\)を出し、\((\hat{p}_{c,+h} - \hat{p}_{c,-h})/h/2\)をすれば出ます。
4.3 信頼区間
推定した係数の平均と分散共分散行列を使って、mvtnorm::rmvnormで大量の係数のサンプルをつくり、そこから予測確率や限界効果を計算したサンプルをつくり、quantileの引数にprob = c(0.025, 0.975)などをつけて計算結果のサンプルを処理すると大雑把な信頼区間が出ます。
5 順序ロジットモデル（ordered logit）
順序ロジットは、①大好き、②好き、③どちらでもない、④嫌い…と言うような、順序は分かるが数量ではないデータを、従属変数として扱う回帰分析です。それぞれ選択肢と言うかカテゴリーがとる確率は非負で、また合計は1になり、さらに選択肢と選択肢の差は一定とは限らないため、普通の線形回帰は用いることができないため、アンケートデータの分析の定番手法となっています。
典型的な順序データの分析で簡素なものは、個人\(i\)が、\(J\)種類の選択肢の中から\(j\)を選ぶ確率\(\pi_{ij}\)を、\(\pi_{ij} = P(\gamma_{j}-x_i\beta) - P(\gamma_{j-1}-x_i\beta)\)と考えます。\(1 \leq j < J\)では\(P\)は値枠が0から1までの単調増加関数で、要するに何か累積分布関数です。手計算で用意に微分ができるロジスティック分布の確率密度関数\(P(y) = 1/(1 + \exp(y)^{-1}\))がよく用いられています。ただし、\(j=0\)のとき0、\(j=J\)のときは1とします。
係数ベクトル\(\beta\)と\(\gamma\)の推定は最尤法を用います。尤度関数は、サンプルサイズを\(n\)、\(I(j=k)\)を\(j=k\)のとき1、\(j
\ne k\)のとき0とする単関数として、\(\Pi_{i=1}^n
\pi_{i1}^{I(j=1)}\pi_{i2}^{I(j=2)}\cdots\pi_{iJ}^{I(j=J)}\)です。間違いがないようにordinal::clmやMASS::polrなどによる推定を推奨しますが、Rのnlm関数やoptim関数あたりに対数尤度関数を与えて推定することも、そんなに難しくは無いです。
MASS::polrを使って推定してみます。なお、GLMではなくて、最尤法による推定です。
df01 <- read.table("https://wh.anlyznews.com/R/dataset/for_ologit.txt", sep = "\t", header = TRUE)
df01$g <- ordered(df01$g, c("d", "c", "b", "a")) # 順序データにする; 序列はアルファベット順と逆
library(MASS)
次のパッケージを付け加えます: 'MASS'以下のオブジェクトは 'package:dfidx' からマスクされています:
selectCall:
polr(formula = g ~ x1 + x2 + d, data = df01, Hess = TRUE)
Coefficients:
Value Std. Error t value
x1 -3.9392 0.8575 -4.5937
x2 4.6511 0.8431 5.5165
dphoenix 0.2306 0.5333 0.4324
dtiger -1.2238 0.5121 -2.3898
Intercepts:
Value Std. Error t value
d|c -1.7854 0.6811 -2.6213
c|b -0.4622 0.6340 -0.7290
b|a 1.5432 0.6675 2.3117
Residual Deviance: 197.8555
AIC: 211.8555 信頼区間は二項ロジットと同様にconfint(r_polr)で出ます。
5.1 限界効果
限界効果も二項ロジットと同様に計算できます。
library(effects)
r_pe <- predictorEffects(r_polr, ~ x1 + x2, confidence.level = 0.99)
plot(r_pe, axes = list(grid = TRUE))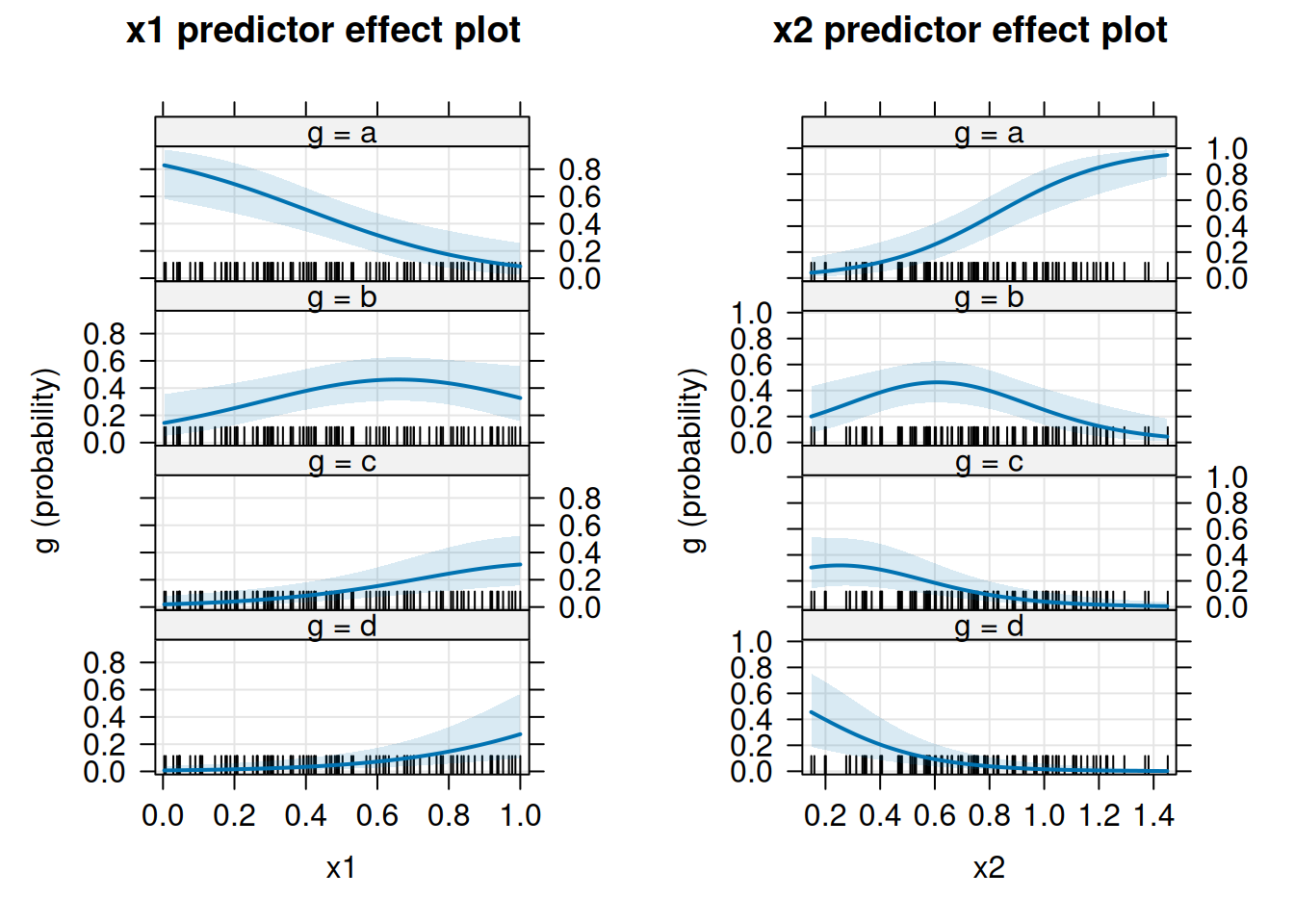
Term Group Contrast Estimate Std. Error z Pr(>|z|) S 2.5 %
d d phoenix - dragon -0.0129 0.0301 -0.429 0.6678 0.6 -0.07180
d d tiger - dragon 0.1052 0.0448 2.345 0.0190 5.7 0.01728
d c phoenix - dragon -0.0128 0.0296 -0.430 0.6670 0.6 -0.07084
d c tiger - dragon 0.0631 0.0306 2.061 0.0393 4.7 0.00310
d b phoenix - dragon -0.0130 0.0302 -0.430 0.6670 0.6 -0.07229
d b tiger - dragon 0.0353 0.0209 1.686 0.0918 3.4 -0.00572
d a phoenix - dragon 0.0387 0.0894 0.432 0.6655 0.6 -0.13661
d a tiger - dragon -0.2035 0.0806 -2.525 0.0116 6.4 -0.36150
x1 d dY/dX 0.3006 0.0842 3.572 <0.001 11.5 0.13565
x1 c dY/dX 0.2273 0.0632 3.595 <0.001 11.6 0.10338
x1 b dY/dX 0.1135 0.0539 2.104 0.0353 4.8 0.00779
x1 a dY/dX -0.6414 0.1104 -5.811 <0.001 27.3 -0.85779
x2 d dY/dX -0.3549 0.0926 -3.831 <0.001 12.9 -0.53651
x2 c dY/dX -0.2684 0.0667 -4.026 <0.001 14.1 -0.39904
x2 b dY/dX -0.1340 0.0553 -2.422 0.0154 6.0 -0.24245
x2 a dY/dX 0.7573 0.0736 10.287 <0.001 80.0 0.61305
97.5 %
0.0460
0.1930
0.0453
0.1231
0.0463
0.0762
0.2139
-0.0456
0.4656
0.3513
0.2192
-0.4251
-0.1734
-0.1377
-0.0256
0.9016
Type: probs5.2 最適化関数を使った推定
Rの行列のデータ構造を活かして行列で処理するところをベクトルで処理してループを削減したため見通しが悪いですが、意外に簡単に推定できます。
llf <- function(p){
ng <- max(s_id) - 1
g <- p[1:ng]
if(2 <= ng) for(i in 2:ng) if(g[i] <= g[i-1]) return(-Inf)
b <- p[-c(1:ng)]
y <- X %*% b
n <- nrow(X)
a <- matrix(g, n, length(g), byrow = TRUE) - replicate(length(g), c(y))
p <- 1/(1 + 1/exp(a))
dp <- cbind(p, 1) - cbind(0, p)
r <- sum(log(dp[1:nrow(dp) + nrow(dp)*(s_id - 1)]))
}
mf <- model.frame(g ~ x1 + x2 + d, df01)
s_id <- as.integer(model.response(mf))
X <- model.matrix(terms(mf), mf)
init.p <- c(seq(3, 5, length.out = max(s_id) - 1), rep(1, ncol(X)))
r_optim <- optim(init.p, llf, method = "L-BFGS-B", control = list(fnscale = -1))
# 閾値-切片項と変数の係数
with(r_optim, c(par[1:3] - par[4], par[5:8]))[1] -1.7853543 -0.4621157 1.5432442 -3.9394564 4.6513028 0.2306246 -1.2237194MASS::polrとほぼ同じ推定結果になっていますね。ordinal::clmかMASS::polrを使いましょう。
Polson, Scott and Windle (2013)がロジスティック関数をPolya-Gamma分布で表現する手法を提案するまで、ロジスティック関数をMCMCのギブズサンプラーでうまくサンプリングすることができなかったため、ベイズ統計学ではプロビットの方が人気だと言う話もあります。↩︎
Train (1993) “Qualitative Choice Analysis: Theory, Econometrics, and an Application to Automobile Demand,” Cambridge: The MIT Pressの第2章↩︎
例えばサンプルサイズ\(n\)の指数分布の最大値から\(\log n\)を減じた値は、\(n\rightarrow\infty\)のとき、標準ガンベル分布に従います。↩︎
マルコフ連鎖モンテカルロのギブスサンプラーを使おうとするとデータ拡大法でプロビットモデルの方が扱いやすくなるので、必ずそうとも言えなかったりします。↩︎
GLMは指数分布族の確率分布のモデルに対して使うことができ、フィッシャー情報行列でヘッセ行列を置き換えることで、二階微分が不要になっているスコア推定のことです。ウェイト付線形回帰の形式に持っていけることから、一般線形モデル（OLS）の拡張となります。詳細はドブソン『統計モデル入門』の第3章と第4章と関連した付録AとBを参照してください。↩︎
疫学ではconditional logitを縦断データのための拡張を指すそうです。疫学のための
survivalパッケージの中のclogit関数が社会科学の方言での意味でのconditional logit modelでの推定に使えたりしますが。↩︎統計学者の書き物でもこの意味でmixied logitと呼んでいるときがあるのですが、統計学の論文では係数が定数ではなく分布で与えられる場合をmixed logitと呼んでいます。なお、
mlogitパッケージは係数が確率分布に従うとするrandom parameters logit modelもサポートしています。↩︎車での所要時間と電車での所要時間の二つの変数を入れれば済みそうですが、
mlogitパッケージは指定できるようになっています。↩︎計量経済学におけるロジスティックモデルの応用のチートペーパーになっているので、経済学徒は目を通しておくとよいかも知れません。↩︎
方程式ごとに誤差項の分散が異なる一方、完全には独立ではないことを仮定し、FGLSで推定する方法です。
systemfitパッケージで簡単に推定することができます。↩︎