観測値の従属変数が非負の整数のデータはよくあります。何かの発生件数などのカウントデータでは、観測値に\(0\)や\(1\)が多数ある場合も多いです。しかし、予測値が\((-\infty, \infty)\)のOLSでは、上手く当てはまりません。
1 ポアソン回帰モデル
もっともよく知られたカウントデータの推定方法は、観測値が非負の整数となるポアソン分布のパラメーターを推定するポアソン回帰モデルです。統計学の教科書では馬に蹴られて死んだ兵士の数が例に挙げられていたりしますが、サッカーのゴール数なども従い、この世に広く見られる分布です。
1.1 分布の導出
推定を行う前に、二項分布からポアソン分布を導出し、その性質を確認していきましょう。
1.1.1 二項分布
確率\(p\)で生起する場合の二項分布で、n回試行してm回生起する場合の確率質量関数は以下になります。
\[ f^B_X(m) = \begin{pmatrix} n \\ m \end{pmatrix} p^m (1-p)^{n-m} \]
生起確率\(p\)を\(m\)回、不生起確率\(1-p\)を\(n-m\)回乗じるわけですが、生起と不生起の回数だけで確率が定まり、順不同なので、組み合わせの数\({}_nC_m\)も乗じられます。
1.1.2 ポアソン分布
\(n\)がとても大きくなると\({}_n\!C_m\)の計算が困難になり、二項分布は実用的でなくなります。しかし\(n\)を無限大と看做したときの確率質量関数を考えると、\({}_nC_m\)が出て来ません。これがポアソン分布です。
導出は、二項分布の平均値\(\lambda\)を考えます。
\[\begin{align} \lambda &= np \\ p &= \frac{\lambda}{n} \end{align}\]
\(\lambda\)と階乗を使って、二項分布の確率質量関数を書き換えます。
\[\begin{align} &f^B_X(m) = \frac{n!}{m!(n-m)!} \bigg( \frac{\lambda}{n} \bigg)^m \bigg(1 - \frac{\lambda}{n} \bigg)^{n-m} \\ &= \frac{n(n-1)\cdots(n-m+1)}{m!} \bigg( \frac{\lambda}{n} \bigg)^m \bigg(1 - \frac{\lambda}{n} \bigg)^{n-m} \\ &= (1)(1 - \frac{1}{n}) \cdots (1 - \frac{m - 1}{n}) \frac{1}{m!} n^m \bigg( \frac{\lambda}{n} \bigg)^m \bigg(1 - \frac{\lambda}{n} \bigg)^n \bigg(1 - \frac{\lambda}{n} \bigg)^{-m} \end{align}\]
ここで、
\[\begin{align} \lim_{n\rightarrow\infty} (1 - \frac{1}{n}) \cdots (1 - \frac{m - 1}{n}) &= 1 \\ \lim_{n\rightarrow\infty} \bigg(1 - \frac{\lambda}{n} \bigg)^n &= \exp(-\lambda) \\ \lim_{n\rightarrow\infty} \bigg(1 - \frac{\lambda}{n} \bigg)^{-m} &= 1 \end{align}\]
に注意すると、
\[ \lim_{n\rightarrow\infty} f^B_X(m) = \frac{1}{m!} \lambda^m \exp(-\lambda) \]
となります。ポアソン分布の確率質量関数が導出できました。
二項分布とポアソン分布の確率質量関数を並べて、ポアソン分布が二項分布のそれらしい近似になっていることを確認しましょう。
m <- 0:10; n <- 10; p <- 0.2;
lambda <- n*p;
M <- matrix(c(dbinom(m, n, p), dpois(m, lambda)), length(m), dimnames = list(m = m, dist = c(sprintf("B(%d, %.2f)", n, p), sprintf("Pois(%.2f)", lambda))))
barplot(t(M), beside = TRUE, legend.text = TRUE, args.legend = list(x = "topright"), xlab = "m", ylab = "probability")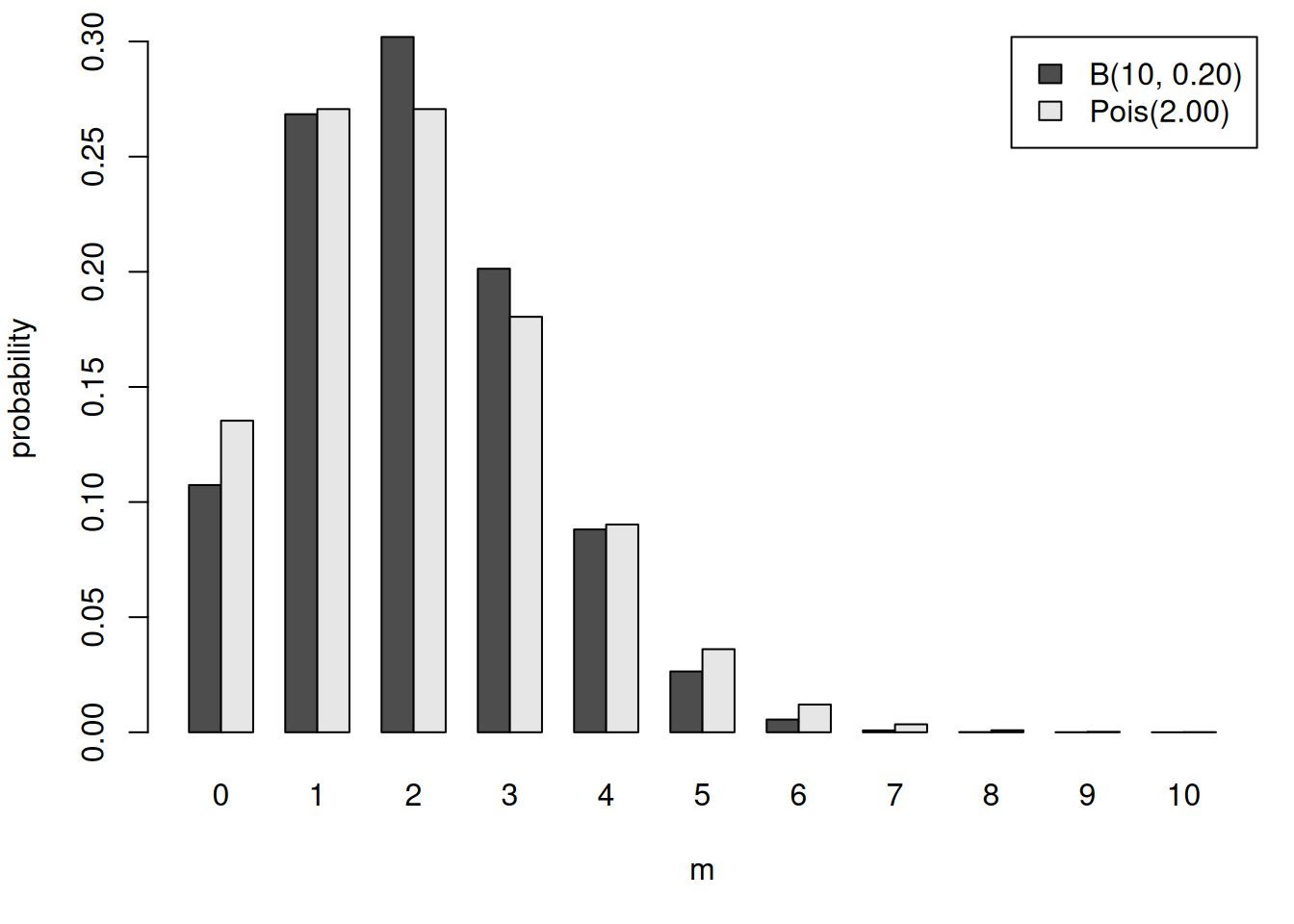
1.1.2.1 \(\lim_{n\rightarrow\infty} \big(1 - \frac{\lambda}{n} \big)^n = \exp(-\lambda)\)の導出
中高で教わる範囲内ですが、指数まわりが変則的なので補足を書いておきます。
ネイピア数を、微分で不変になる指数関数の底と定義します。
\[ \lim_{h \rightarrow 0} \frac{\exp(x + h) - \exp(x)}{h} = \exp(x) \]
となるので、両辺を\(\exp(x)\)と割ると
\[\begin{align} \lim_{h \rightarrow 0} \frac{\exp(h) - 1}{h} = 1 \end{align}\]
となります。\(y\)を\(\exp(h) - 1\)と定義すると、
\[\begin{align} \exp(h) &= y + 1 \\ h &= \log(1 + y) \end{align}\]
となります。
\[ \lim_{h \rightarrow 0} \exp(h) = y + 1 = 1 \]
となるので、\(h \rightarrow 0 \Leftrightarrow y \rightarrow 0\)です。
\(\lim_{h \rightarrow 0} (\exp(h) - 1)/h = 1\)を書き直して整理します。
\[\begin{align} \lim_{y \rightarrow 0} \frac{y}{\log(1+y)} &= 1 \\ \lim_{y \rightarrow 0} \frac{\log(1+y)}{y} &= 1 \\ \lim_{y \rightarrow 0} (1 + y)^\frac{1}{y} &= e \end{align}\]
\(z=1/y\)と置いて、さらに整理します。
\[ \lim_{z \rightarrow \infty} (1 + \frac{1}{z})^{z} = e \]
\(z \rightarrow -\infty\)の場合も整理しておきましょう。
\[\begin{align} \lim_{z \rightarrow -\infty} (1 + \frac{1}{z})^{z} &= \lim_{z \rightarrow \infty} (1 - \frac{1}{z})^{-z} \\ &= \lim_{z \rightarrow \infty} \bigg( \frac{z}{z-1} \bigg)^{z} \ \ \mbox{(分子と分母を入れ替え、指数のマイナス符号をとる)} \\ &= \lim_{z \rightarrow \infty} \bigg( 1 + \frac{1}{z - 1} \bigg)^{z - 1} \bigg( 1 + \frac{1}{z - 1} \bigg) \\ &= e \end{align}\]
上の一部を切り出し、\(z=n/\lambda\)と置くと、\(\lambda\)が定数なので\(n \rightarrow \infty \Rightarrow z \rightarrow \infty\)になるので、ポアソン分布の導出に使った式になります。
\[\begin{align} \lim_{n \rightarrow \infty} (1 - \frac{1}{n/\lambda})^{-n/\lambda} &= e \\ \bigg( \lim_{z \rightarrow \infty} (1 - \frac{1}{n/\lambda})^{-n/\lambda} \bigg)^\lambda &= e^\lambda \end{align}\]
1.2 ポアソン分布の期待値と分散
ポアソン分布には、実データの分析で問題になる性質があるので確認しておきます。
ポアソン分布のモーメント母関数を考えます。
\[\begin{align} M_X(t) &= E\big[ \exp(tm) \big] \\ &= \sum^{\infty}_{m=0} \exp(tm) \frac{1}{m!} \lambda^m \exp(-\lambda) \\ &= \exp(-\lambda) \sum^{\infty}_{m=0} \exp(tm) \frac{1}{m!} \lambda^m \end{align}\]
指数関数のマクローリン展開から、
\[ \exp(\lambda \exp(t)) = \sum^{\infty}_{m=0} \frac{\lambda^m \exp(tm)}{m!} \]
になることに注意すると、
\[\begin{align} M_X(t) &= \exp(-\lambda) \exp(\lambda \exp(t)) \\ &= \exp(\lambda(\exp(t) - 1)) \end{align}\]
となります。
モーメント母関数を\(t\)で一階微分して\(t=0\)とすれば期待値、二階微分して\(t=0\)とし、期待値の二乗を引けば分散が計算できます。
\[\begin{align} \left. \frac{dM_X(t)}{dt} \right|_{t=0} &= \lambda \exp(t + \lambda (\exp(t) - 1)) \mid_{t=0} \\ &= \lambda \end{align}\]
\[\begin{align} \left. \frac{d^2M_X(t)}{dt^2} \right|_{t=0} &= \lambda (1 + \lambda \exp(t))\exp(t + \lambda(\exp(t) - 1)) \mid_{t=0} \\ &= \lambda^2 + \lambda \end{align}\]
期待値も分散も\(\lambda\)になることが分かりました。パラメーターがひとつであることから自明ではあるのですが、柔軟性に欠けることが分かります。
1.3 推定
従属変数がポアソン分布に従うとして、ポアソン分布のパラメーター\(\lambda\)を推定すれば、ポアソン回帰になります。\(\lambda\)を説明するモデルを仮定し、最尤法か一般化線形モデル(GLM)1で推定します。
1.3.1 計量モデル
よく使われるモデルが対数線形モデルです。\(i\)を個体、\(X\)が説明変数の行列、\(\beta\)をその係数ベクトルとして、
\[ \log \lambda_i = X_i\beta \]
と定義されます。\(\lambda_i\)の予測値は\(\exp(X_i\beta)\)と、必ず非負になります。ポアソン分布の期待値は非負ですから都合がよくなります。
平方根モデルも、予測値は非負になります。線形予測を二乗するからです。
\[ \sqrt{\lambda_i} = X_i\beta \]
線形モデル\(\lambda = X\beta\)は直感的ですが、場合によっては負の値が出てきて推定がおかしくなります。
1.3.2 オフセット項
市町村ごとの事故や事件や病気の件数は、市町村の人口に大きく左右されますが、ポアソン分布の期待値を何かで割ったものを予測したほうがよいかも知れません。その場合は、オフセット項付きポアソン回帰を用います。
\[ \log \lambda_i = X_i\beta + \log \mbox{offset}_i \]
何を意味するのか分かりづらいかも知れませんが、
\[\begin{align} \log \lambda_i - \log \mbox{offset}_i &= X_i\beta \\ \log \frac{\lambda_i}{\mbox{offset}_i} &= X_i\beta \\ \frac{\lambda_i}{\mbox{offset}_i} &= \exp(X_i\beta) \end{align}\]
オフセット項に対する平均値を指数関数で表したものになります。
1.3.3 GLMによる推定
glmコマンドを使うと、簡単にGLMで推定できます。リンク関数の導出などは不要です。
# データをロード
df01 <- read.table("https://wh.anlyznews.com/R/dataset/for_poisson.txt", sep = "\t", header = TRUE)
# 対数線形モデルになるリンク関数を指定
summary(r_poi <- glm(y ~ x + z, poisson(link = "log"), data = df01))
Call:
glm(formula = y ~ x + z, family = poisson(link = "log"), data = df01)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.75081 0.01448 328.08 <2e-16 ***
x 1.62705 0.02717 59.88 <2e-16 ***
z -0.76750 0.02273 -33.77 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 12377.4 on 49 degrees of freedom
Residual deviance: 8028.4 on 47 degrees of freedom
AIC: 8313.4
Number of Fisher Scoring iterations: 6# 列oの対数をオフセット項にする
summary(r_poi_o <- glm(y ~ x + z + offset(log(o)), poisson(link = "log"), data = df01))
Call:
glm(formula = y ~ x + z + offset(log(o)), family = poisson(link = "log"),
data = df01)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.004313 0.015027 0.287 0.774
x 2.250706 0.030490 73.817 <2e-16 ***
z -0.920329 0.026781 -34.365 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 8637.0 on 49 degrees of freedom
Residual deviance: 1691.5 on 47 degrees of freedom
AIC: 1976.5
Number of Fisher Scoring iterations: 5link = "log"をlink = "sqrt"にすると平方根モデル、link = "identity"にすると線形モデルになります。GLMも反復して解に接近する手法で、ごく稀に初期値によって収束しないときがあります。その場合はstart引数で初期値を指定できます。
オフセット項はoffset = log(o)というように、引数でも指定できます。
1.3.4 over-dispersion test
ポアソン分布はパラメーターひとつで期待値と分散をあらわす分布なので、データがそれにあてはまると看做せないときもあります。つまり、過分散の問題が出ることがあります。
予測値の大きさと残差の絶対値に相関がある場合、ポアソン分布の仮定を満たしていないことが分かります。以下の線形回帰で\(z\)の係数が0を棄却されたら、つまり有意に0以外ならば分散が過小もしくは過大で、ポアソン分布でないと看做すことになります。
lambda <- fitted.values(r_poi_o)
z <- with(df01, ((y - lambda)^2 - y)/(lambda * sqrt(2)))
summary(lm(z ~ 1))
Call:
lm(formula = z ~ 1)
Residuals:
Min 1Q Median 3Q Max
-25.27 -24.68 -21.78 -14.24 513.63
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 24.56 11.41 2.154 0.0362 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 80.65 on 49 degrees of freedom上のコードの他にも幾つか手法があります。AER::dispersiontestやoverdisp::overdispなどパッケージで関数が提供もされています。
過分散が生じているということは、標準誤差が過小に推定されていることになります。統計的仮説検定が偽陽性になり、信頼区間が狭くなりがちです。
1.3.5 最尤法による推定
(対数)尤度関数を書けば、optimなどの最適化アルゴリズムを用いて推定することもできます。GLMの説明を避けたい場合は、有用かも知れません。
# offset項ありモデル
mf <- model.frame(y ~ x + z + offset(log(o)), data = df01)
X <- model.matrix(terms(mf), mf)
y <- model.response(mf)
log_o <- model.offset(mf)
llf <- function(p){
lambda <- exp(X %*% p + log_o)
# sum(dpois(y, lambda, log = TRUE))
sum(y*log(lambda) - lambda - lgamma(y + 1))
}
# グラディエント関数を定義すると速度が向上し、収束しない可能性が減る(が通常は不要)
llfg <- function(p){
lambda <- exp(X %*% p + log_o)
dlambda <- apply(X, 2, \(x) x*lambda)
apply(y*X - dlambda, 2, sum)
}
init.p <- c(1, 1, 1)
(r_optim <- optim(init.p, llf, llfg, method = "BFGS", control = list(fnscale = -1, reltol = 1e-8)))$par
[1] 0.004313073 2.250705879 -0.920328573
$value
[1] -985.2519
$counts
function gradient
59 12
$convergence
[1] 0
$message
NULL2 擬似ポアソン回帰モデル
過分散の対策としては、擬似ポアソン回帰モデルがあります。係数の推定はポアソン回帰と同様ですが、分散の推定量をdispersion parameterと呼ばれる\(\hat{\phi}\)でスケールします。
\[ \hat{\phi} = \frac{\sum^n_i (y_i - \hat{\lambda}_i)^2 / \hat{\lambda}_i}{\mbox{df}} \]
分子はピアソンのχ二乗統計量です。\(\mbox{df}\)は(残差の)自由度で、標本サイズからパラメーターの数を引いた数になります。
よって、Rでは以下のように計算できます。
どう使えばいいのか感がありますが、推定結果の要約を出すときに推定したdispersion parameterを指定できるので、難しくはありません。
Call:
glm(formula = y ~ x + z + offset(log(o)), family = poisson(link = "log"),
data = df01)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.004313 0.092683 0.047 0.963
x 2.250706 0.188063 11.968 < 2e-16 ***
z -0.920329 0.165185 -5.571 2.53e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 38.04379)
Null deviance: 8637.0 on 49 degrees of freedom
Residual deviance: 1691.5 on 47 degrees of freedom
AIC: 1976.5
Number of Fisher Scoring iterations: 5分散を\(\lambda\)の\(\phi\)倍しているだけです。
リンク関数をpoissonからquasipoissonに置き換えると、一行で同じ結果が得られます。
Call:
glm(formula = y ~ x + z + offset(log(o)), family = quasipoisson(link = "log"),
data = df01)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.004313 0.092683 0.047 0.963
x 2.250706 0.188063 11.968 7.14e-16 ***
z -0.920329 0.165185 -5.571 1.19e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasipoisson family taken to be 38.04379)
Null deviance: 8637.0 on 49 degrees of freedom
Residual deviance: 1691.5 on 47 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 5この方法は、係数の推定量と標準誤差を得るためには有用なのですが、厳密には最尤法でもGLMでもなく、AICなどの情報量規準を使ってモデル選択ができないなどの欠点があります。
3 負の二項回帰モデル
過分散の対策としては、ポアソン分布のパラメーター\(\lambda\)が何かの分布に従う確率変数と考え、推定モデルを階層化する方が望ましいです。典型的には、\(\lambda\)がガンマ分布に従うと仮定し、負の二項分布を導出してポアソン分布の代わりに使います。
3.1 分布の導出
一定確率の試行が一定回数成功するまでの、試行回数の分布として知られる負の二項回帰が、ポアソン分布の拡張になるのは直感的とは言い難いですが、そうなることを計算して確認しましょう。以下では、指数分布を導出したあと、指数分布の和としてガンマ分布を導出し、ポアソン分布とガンマ分布から負の二項分布を導出します。
3.1.1 指数分布
指数分布は、確率変数が大きくなるにつれて、確率密度が定率で減っていく場合に用いられます。典型的には、時間あたりに一定の確率で起きる事象が1回以上生起した割合を、その累積分布関数で示したいときに用います。
累積分布関数を\(F(\lambda)\)と置きます。\(\lambda\)は時間で、台が\([0, \infty)\)になります。時点\(\lambda\)まで事象が生じなかった確率は、\(1 - F(\lambda)\)です。
時点\(\lambda\)から\(\lambda+d\lambda\)までの間に事象が生じる確率は、\(F(\lambda+d\lambda) - F(\lambda)\)もしくは、\((1 - F(\lambda))(F(d\lambda) - F(0))\)となります。時間あたりの発生率は一定なので、未生起の中で\(d\lambda\)の間に生起する割合は、常に\(F(d\lambda)\)だからです。
\[\begin{align} F(\lambda+d\lambda) - F(\lambda) &= (1 - F(\lambda))(F(d\lambda) - F(0)) \\ \lim_{d\lambda \rightarrow 0} \frac{F(\lambda+d\lambda) - F(\lambda)}{d\lambda} &= (1 - F(\lambda)) \lim_{d\lambda \rightarrow 0} \frac{F(d\lambda) - F(0)}{d\lambda} \\ F'(\lambda) &= (1 - F(\lambda))F'(0) \end{align}\]
となるので、定数になる\(F'(0)\)を\(\beta\)と置いて、この微分方程式を解きます。
\[\begin{align} \frac{F'(\lambda)}{1 - F(\lambda)} &= \beta \\ \int \frac{F'(\lambda)}{1 - F(\lambda)} &= \int \beta d\lambda \\ - \log (1 - F(\lambda)) &= \beta \lambda \\ (1 - F(\lambda)) &= \exp(- \beta \lambda) \\ F(\lambda) &= 1 - \exp(- \beta \lambda) \\ F'(\lambda) &= \beta \exp(- \beta \lambda) \end{align}\]
確率密度関数\(\beta \exp(- \beta \lambda)\)と、累積分布関数\(1 - \exp(- \beta \lambda)\)が導出できました。
3.1.2 ガンマ分布
指数分布に従う2つの確率変数の合計\(y\)が従う分布を考えます。片方の変数を\(x_1\)と置いて、畳み込み計算をすると、
\[\begin{align} \int_0^y \beta \exp(-\beta(y - x_1))\beta\exp(-\beta x_1) dx_1 = \beta^2 y \exp(-\beta y) \end{align}\]
と導出できます。この確率密度に従う確率変数\(y\)と指数分布に従う\(x_2\)の合計\(z\)の確率密度関数は、同様に、
\[\begin{align} &\int_0^z \beta^2 (z - x_2) \exp(-\beta(z - x_2))\beta\exp(-\beta x_2) dx_2 \\ &=\beta^3 \frac{z^2}{2} \exp(-\beta z) \end{align}\]
\(\alpha\)個の指数分布の和の確率密度関数が\(\beta^\alpha \frac{\lambda^{\alpha-1}}{(\alpha-1)!} \exp(-\beta \lambda)\)と書けるとき、\(\alpha+1\)個の指数分布の和の確率密度関数は、
\[\begin{align} &\int_0^\lambda \beta^\alpha \frac{(\lambda - x_3)^{\alpha-1}}{(\alpha-1)!} \exp(-\beta \lambda - x_3) \beta \exp(- \beta x_3) \\ &= \beta^{\alpha+1} \frac{\lambda^{\alpha}}{\alpha!} \exp(-\beta \lambda) \\ &= \beta^{\alpha+1} \frac{\lambda^{\alpha}}{\Gamma(\alpha + 1)} \exp(-\beta \lambda) \end{align}\]
よって数学的帰納法で、\(\alpha\)個のパラメーター\(\beta\)の指数分布に従う確率変数の合計\(\lambda\)の確率密度は、
\[\begin{align} f_X^{G}(\lambda) = \beta^{\alpha} \frac{\lambda^{\alpha - 1}}{\Gamma(\alpha)} \exp(-\beta \lambda) \end{align}\]
とガンマ関数の確率密度になることが分かります。
なお、ガンマ関数のパラメーターは実数であるので、ここではガンマ分布の特殊形になっていることには注意してください。負の二項回帰分布の導出に使うガンマ関数は、この特殊形で間に合いますが、厳密には指数分布をガンマ分布のひとつと捉え、ガンマ分布の再生性2から指数分布に従う確率変数の合計値はガンマ分布に従うと考える必要があります。
3.1.3 負の二項分布
ポアソン分布の確率密度関数を再掲します。
\[ f_X^P(m) = \frac{1}{m!} \lambda^m \exp(-\lambda) \]
ポアソン分布のパラメーター\(\lambda\)がガンマ分布に従うときの確率質量関数は、
\[ f^{NB}_X(m) = \int_0^\infty f_X^P(m) f_X^{G}(\lambda) d\lambda \]
となります。\(\lambda\)で積分をして、\(\lambda\)を消します。
\[\begin{align} &= \int_0^\infty \frac{1}{m!} \lambda^m \exp(-\lambda) \frac{\beta^\alpha}{\Gamma(\alpha)}\lambda^{\alpha-1}\exp(-\beta\lambda) d\lambda \\ &= \frac{\beta^\alpha}{x! \Gamma(\alpha)} \int_0^\infty \lambda^{m + \alpha - 1} \exp(-(\beta + 1)\lambda) d\lambda \\ &= \frac{\beta^\alpha}{x! \Gamma(\alpha)} \frac{\Gamma(m + \alpha)}{(\beta + 1)^{m + \alpha}} \int_0^\infty \frac{ (\beta + 1)^{m + \alpha} \lambda^{m + \alpha - 1} \exp(-(\beta + 1)\lambda) }{\Gamma(m + \alpha)} d\lambda \end{align}\]
\(k = m + \alpha\), \(c = \beta + 1\)と置くと、積分の中が\(c^{k}\lambda^{k+1}\exp(-c\lambda)/\Gamma(k)\)となり、ガウス分布の確率密度関数なのが分かります。よって、\([0, \infty)\)で積分すると\(1\)になります。
\(\alpha\)は整数と仮定すると、ガンマ関数を階乗に変換できます。
\[\begin{align} &= \frac{\beta^\alpha}{m!(\alpha - 1)!} \frac{(m + \alpha - 1)!}{(\beta + 1)^{m + \alpha}} \\ &= \frac{(m + \alpha - 1)!}{m!(\alpha - 1)!} \beta^\alpha (\beta + 1)^{-(m + \alpha)} \\ &= \begin{pmatrix} m + \alpha - 1 \\ \alpha - 1 \end{pmatrix} \beta^\alpha (\beta + 1)^{-(m + \alpha)} \end{align}\]
\(\beta = p/(1-p)\)と置くと、
\[\begin{align} &= \begin{pmatrix} m + \alpha - 1 \\ \alpha - 1 \end{pmatrix} \bigg( \frac{1-p}{p} \bigg)^\alpha p^{m + \alpha} \\ &= \begin{pmatrix} m + \alpha - 1 \\ \alpha - 1 \end{pmatrix} p^\alpha (1-p)^m \end{align}\]
と負の二項分布の確率質量関数が導出できます。
3.2 計量モデル
負の二項分布だと分かるように導出しましたが、線形予測部分は期待値を説明するので、このままでは推定できません3。期待値\(\mu\)とシェープ\(\theta\)で書き直します4。
\[ f^{NB}_X(m) = \frac{\Gamma(m + \theta)}{\Gamma(\theta)m!}\frac{\mu^m \theta^\theta}{(\mu + \theta)^{m + \theta}} \]
ポアソン回帰と同様に、\(\mu\)を対数線形回帰などで予測できるとして推定します。
3.3 変則GLMによる推定
RではMASS::glm.nbで負の二項分布を推定できます。family = negative.binomial(theta = 1)というように\(\theta\)を固定したリンク関数をGLMに与えて線形予測部分を推定し、線形予測部分を固定して\(\theta\)を推定することを交互に行う、EMアルゴリズム的な方法をとっているそうです。
Call:
glm.nb(formula = y ~ x + z + offset(log(o)), data = df01, init.theta = 4.310738114,
link = log)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.01743 0.07464 0.233 0.815
x 1.94193 0.15189 12.785 <2e-16 ***
z -1.09089 0.13171 -8.283 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for Negative Binomial(4.3107) family taken to be 1)
Null deviance: 257.798 on 49 degrees of freedom
Residual deviance: 54.469 on 47 degrees of freedom
AIC: 469.73
Number of Fisher Scoring iterations: 1
Theta: 4.311
Std. Err.: 0.992
2 x log-likelihood: -461.725 推定結果を見ると\(\hat{\theta}\)が整数ではありません。実のところ、拡張された負の二項分布を使っています。不連続なパラメーターは推定しづらいですからね。
GLMは指数分布族の確率分布のモデルに対して使うことができ、フィッシャー情報行列でヘッセ行列を置き換えることで、二階微分が不要になっているスコア推定のことです。ウェイト付線形回帰の形式に持っていけることから、一般線形モデル(OLS)の拡張となります。詳細はドブソン『統計モデル入門』の第3章と第4章と関連した付録AとBを参照してください。↩︎
\(\beta\)が同じガンマ分布のモーメント母関数の積は、やはりガンマ分布のモーメント母関数になります。↩︎
\(\mu = m(1-p)/p\), \(\theta = \alpha - 1\)と書けるので、最尤法で推定するときは、本文中の式を導出する必要は無いです。↩︎
Zeileis, Kleiber and Jackman (2008) "Regression Models for Count Data in R," Journal of Statistical Software, 27(8), pp.1–25. https://doi.org/10.18637/jss.v027.i08↩︎
