最も基本的な回帰分析になる一般線形回帰(OLS)は、データフレームにデータセットがまとまっていれば、関数一つで計算できますが、出てきた推定結果を使いまわすにはもう少し命令を書かないといけません。必要な関数がひとつのヘルプにまとまっておらず、見落としがち、忘れがちなので、まとめておきます。
1 OLSとは
コーディングの説明に入る前に、OLSの復習をしましょう。後で何をしているのか分からなくなるのを防止する効果があります。概要を触れるだけなので、詳しい説明は計量分析の教科書1を参照してください。
以下のような線形モデルの最小二乗法による推定を、OLSと呼んでいます。
\[ y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_{k-1} x_{ik-1} + \epsilon_i \]
\(y\)は被説明変数のベクトル、\(\beta\)は係数、\(x\)は説明変数のベクトル、\(\epsilon\)は誤差項のベクトル、\(i\)はどの観測値かを示す添字、\(j\)はどの説明変数かを示す添字になります。観測値の数は\(n\)、係数は\(k\)種類です。各観測値の誤差\(\epsilon_i\)は同一で独立の分布に従います。\(\text{COV}(x_j, \epsilon)=0\)が仮定されていることには注意してください。
なお、小標本では誤差項は正規分布する方が望ましいですが、サンプルサイズがある程度あれば、ガウス=マルコフ定理から平均と分散があれば正規分布でなくても大きな問題はありません。
1.1 OLS推定量
説明変数の種類が多いと記述と計算が大変なので、行列の形式で書き直します。
\[ y = X\beta + \epsilon \]
ここで、
\[ y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}, X = \begin{bmatrix} 1 & x_{11} & \cdots & x_{1k-1} \\ 1 & x_{21} & \cdots & x_{2k-1} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{nk-1} \end{bmatrix}, \beta = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_{k-1} \end{bmatrix}, \epsilon = \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{bmatrix} \]
です。
最小二乗法なので、誤差項の二乗和が最小になるように推定量を定めます。誤差項の二乗和は、
\[ \epsilon_1 \epsilon_1 + \epsilon_2 \epsilon_2 + \cdots + \epsilon_n \epsilon_n = \begin{bmatrix} \epsilon_1 & \epsilon_2 & \cdots & \epsilon_n \end{bmatrix} \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{bmatrix} = {}^t\!\epsilon \epsilon \]
\[ = {}^t\!(y - X\beta)(y - X\beta) \]
となります。
ここで、係数のベクトル\(\beta\)を、その推定量のベクトル\(b\)に、誤差項のベクトル\(\epsilon\)を、残差のベクトル\(e\)に置き換えます。
\[ {}^t\!e e = {}^t\!(y - Xb)(y - Xb) \]
転置行列の性質に注意すると、
\[ {}^t\!e e = {}^t\!y y - 2{}^t\!y X b + {}^t\!b {}^t\!X X b \]
となります。\({}^t\!X X\)が対称行列であることに注意して、上式をベクトル\(b\)の要素それぞれに関して微分してできたk本の式を合計し整理すると、誤差項の二乗和の最小化の一階条件は、
\[ -2{}^t\!y X + 2 {}^t\!X X b = 0 \]
になり、OLS推定量
\[ b = ({}^t\!XX)^{-1}{{}^t\!Xy} \]
が得られます。
1.2 OLS推定量の分散
\(b\)は推定量なので誤差があり、その分散は係数の推定量のt検定や信頼区間の計算に用いられます。多変量なので分散共分散行列を導出します。
\[ \text{VAR}[ b \mid X ] = E[{}^t\!(b - \beta)(b - \beta) \mid X] \]
\[ = E[({}^t\!XX)^{-1}{{}^t\!X} \epsilon {{}^t\!\epsilon} X ({}^t\!XX)^{-1} \mid X] \]
\[ =({}^t\!XX)^{-1}{{}^t\!X} E[\epsilon {{}^t\!\epsilon} \mid X] X ({}^t\!XX)^{-1} \]
\[ = ({}^t\!XX)^{-1}{{}^t\!X} \sigma^2 I X ({}^t\!XX)^{-1} =\sigma^2 ({}^t\!XX)^{-1} \]
\(I\)は\(k \times k\)の恒等行列です。
1.3 自由度と分散の不偏推定量
\(\text{VAR}[ b \mid X ]\)の計算に\(\sigma^2\)が必要なので、\(\sigma^2\)の不偏推定量\(s^2\)を考えます。residual maker
\[ M=I-X({}^t\!XX)^{-1}({}^t\!X) \]
を用いると、残差は
\[ e = My = M(X\beta + \epsilon) = M\epsilon \]
と書けます。\(MX=0\)になるからです。さらに\({}^t\!MM=M\)である事に注意すると、
\[ ^t\!ee = {}^t\!\epsilon M \epsilon \]
となります。残差の二乗和の期待値は、
\[ E[{}^t\!ee \mid X] = E[ {}^t\!\epsilon M \epsilon \mid X] \]
となります。\({}^t\!\epsilon M \epsilon\)は\(1 \times 1\)行列になるのでトレースと等しくなり、\({}^t\!\epsilon\)と\(M\)と\(\epsilon\)は循環性を持つことが分かります。
\[ E[ {}^t\!\epsilon M \epsilon \mid X] = E[ tr({}^t\!\epsilon M \epsilon) \mid X] = E[ tr( M \epsilon {}^t\!\epsilon )\mid X] \]
さらに整理し、
\[ =tr( M E[ \epsilon {}^t\!\epsilon \mid X]) = tr( M \sigma^2 I) = \sigma^2 tr(M) \]
\(M\)の定義から、
\[tr(M)=tr(I-X({}^t\!XX)^{-1}({}^t\!X))\]
\[=tr(I_n)-tr(X({}^t\!XX)^{-1}({}^t\!X))\]
\[=tr(I_n)-tr(I_k)\]
\[=n-k\]
よって、
\[E[{}^t\!ee \mid X] = \sigma^2 (n-k)\]
\[s^2 = {}^t\!ee/(n-k)\]
となります。自由度は\(n-k\)です。
2 OLSで推定してみる
タブ区切りのテキストファイルにまとまっているデータセットをデータフレームに読み込んで、OLSで推定してみましょう。
2.1 データセットの読み込み
話の都合上、欠損値などがないデータセットを読み込みます。
テキストファイルからread.tableを使ってデータを読むのが典型的でしたが、最近はreadrパッケージを使う紹介が増えています。
2.2
lmで推定を行なう
テキストでは長々と推定量の導出を行なうわけですが、以下の一行で終わります。
y ~ x + zはモデル式と言われるデータで、変数に入れておいて使いまわす事ができます。
モデル式が入った変数は、異なるデータセットで推定を繰り返すときに便利に使えます。
2.2.1 ダミー変数の作り方
データに応じて1もしくは0の値をとる変数をダミー変数と呼びます。
回答がyesの場合は1、noの場合は0と言うようなのは取り扱いが簡単ですが、年次ダミーの場合は年ごとにダミー変数を、個体ダミーの場合は個体ごとにダミー変数をつくる必要があります。例えば、2000年から2022年までの年次ダミーを入れると、(2000年の分は省略できるので)22のダミー変数がいります。都道府県ダミーをつくると、46のダミー変数がいります。
データフレームの列の値に応じてifelse関数などで1か0の出力してダミー変数をつくって、ダミー変数名をモデル式に長々と書いても問題ないのですが、手間暇がかかります。Rではもっと楽にダミー変数を入れる方法があって、例えばデータフレームのans列の値に応じてダミー変数をつくる場合は、
と書けばダミー変数を入れた推定モデルになります。ansはyesもしくはnoの値をとりますが、1もしくは0として扱ってくれます。なお、ansがfactor属性の場合は、as.factorも要りません。
ans列からのダミー変数とpos列からのダミー変数のクロス項を入れる場合は、
とすれば入ります。
2.2.2 交差項を入れる
以下のように変数名と変数名を*でつないでおくと、それぞれの変数と交差項に展開してくれます。
は、
と同じになります。
2.2.3 変則的な操作
-で変数を除去できます。x + z - xと書くと、zだけの推定と同じになります。
x %in% zは、x:zと同じ結果になります。x %in% ansは、ダミー変数は展開されるので、x:ansno + x:ansyesと同じになります。x %in% (z + ans)のように、右側は複数の変数を括弧でくくることができます。
x/zは、x + x:zに展開されます。x*z - zと書いても同じです。これもx/(z + ans)とも書けます。
(x + z)^2は、x + z + x:zに展開されます。変数の値が二乗されたり、足されたりはしないので、x:xはxと同じとして省略され、z:xはx:zと同じとして省略されます。(x + z + ans)^2や(x + z + ans)^3のような指定も可能です。\(\beta_0 + \beta_1 x^2 + \beta_2 x*z + \beta_3
z^2\)を推定したければ、I(x^2) + x:z + I(z^2)と書く必要があります。
2.2.5 モデル式内での数式
モデル式には対数と四則演算を入れることができます。
例えば\(y = C x^{\beta_1} z^{\beta_2}\)を推定したい場合は、
と書いておくと推定してくれます。
xではなく、x - 1で説明したい場合は、以下のようにします。
2.3 行列演算で推定
もっとも行列演算で行なっても、大したことにはなりません。
r_mc <- with(df01, {
# モデル式から切片項こみの説明変数の行列をつくる
X <- model.matrix(y ~ x + z)
b <- solve(t(X) %*% X) %*% t(X) %*% y
df <- nrow(X) - ncol(X)
sigma2 <- sum((y - X %*% b)^2)/df
vcov <- sigma2*solve(t(X) %*% X)
list(coef = b, vcov = vcov, df = df)
})大したことにならないとは言え、コーディングミスや見通しの問題から、lmを使う方が望ましいです。
3 推定結果の確認と数値の取得
lm関数の戻り値から推定結果を確認するのには、summaryを使います。
Call:
lm(formula = y ~ x + z, data = df01)
Residuals:
Min 1Q Median 3Q Max
-1.30601 -0.57500 0.02577 0.53767 1.92185
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.6368 0.3372 1.889 0.0697 .
x 2.2563 0.2760 8.175 8.85e-09 ***
z -2.5532 0.2712 -9.416 5.08e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8335 on 27 degrees of freedom
Multiple R-squared: 0.8616, Adjusted R-squared: 0.8514
F-statistic: 84.05 on 2 and 27 DF, p-value: 2.54e-12画面に表示するだけではなく、データとして利用もできます。lmやsummaryの戻り値はリスト構造なので、names(lm(...))やnames(summary(lm(...)))でどのような値が使えるか確認できます。
3.1 残差と残差平方和
残差はresiduals(...)で、残差平方和はdeviance(...)で取得できます。
3.2 分散共分散行列
vcov(lm(...))で分散共分散行列を取り出せます。
(Intercept) x z
(Intercept) 0.11368012 -0.082770568 -0.012702326
x -0.08277057 0.076173497 0.005664196
z -0.01270233 0.005664196 0.0735263273.4 決定係数と重相関係数
過適合に上手くペナルティを与えられないため、モデル選択の指標としては、自由度調整をしたものを含めて、決定係数と重相関係数は参照されなくなって久しいですが、従属変数の分散のうち説明変数の分散で説明できる割合を示す分かりやすい指標なので、一応、参照したくなります。
自由度調整済み決定係数をプロットか何かで再利用したい場合は、
[1] 0.851361のようにすれば取得できます。ただの重相関係数はsqrt(summary(...)$r.squared)で取れます。
3.5 係数の推定量
coef(lm(...))で係数の推定量を取り出せます。coef(summary(lm(...)))を用いれば、標準誤差や帰無仮説を0と置いたt値とP値も取り出せます。
(Intercept) x z
0.6368478 2.2562861 -2.5531561 (Intercept) x z
0.3371648 0.2759955 0.2711574 (Intercept) x z
1.888832 8.175084 -9.415772 (Intercept) x z
6.970084e-02 8.845601e-09 5.082933e-10 3.6 係数の推定量の信頼区間
confint(lm(...))で95%信頼区間の計算ができます。引数にlevel = 0.9を加えると90%信頼区間の計算になります。
2.5 % 97.5 %
(Intercept) -0.05495727 1.328653
x 1.68999022 2.822582
z -3.10952510 -1.9967873.7 複数の係数を線形結合した場合のt検定と信頼区間
\(\beta_1 + \beta_2 = 1\)を帰無仮説とした検定を行なう場合などは、やや手の込んだコードを書く必要があります。
やり方は色々だと思いますが、ここでは
# 複数の係数の合算値のt検定を行ない信頼区間を出す関数
ttest <- function(coef, vcov, df, mask, h0 = 0, both = TRUE, a = 0.05){
mask <- matrix(mask, 1, length(mask))
v <- mask %*% vcov %*% t(mask)
se <- sqrt(v)
m <- sum(mask %*% coef)
tv <- (m - h0) / sqrt(v)
tp <- (1 + 1*(both==TRUE))*pt(tv, df, lower.tail = 0>tv)
margin <- qt(1 - a/2, df) * se
list(mean = m, se = se, t_value = tv, p_value = tp, ci = m + c(-margin, margin))
}を用意します。これで簡単に
$mean
[1] -0.29687
$se
[,1]
[1,] 0.4012832
$t_value
[,1]
[1,] 1.752204
$p_value
[,1]
[1,] 0.09109034
$ci
[1] -1.1202351 0.5264952$mean
[1] 4.809442
$se
[,1]
[1,] 0.3719831
$t_value
[,1]
[1,] -0.5122753
$p_value
[,1]
[1,] 0.6126236
$ci
[1] 4.046196 5.572689ことが可能になります。なお、引数maskは係数にかける値のベクトルで、h0が帰無仮説になります。
3.8 偏相関係数
計算してくれる関数は標準では入っていないのですが、以下のようにt値を使って簡単に計算できます2。
(function(r_lm){
s <- summary(r_lm)
t <- coef(s)[,3]
(sign(coef(r_lm))*sqrt(t^2/(t^2 + s$df[2])))[-1]
})(r_lm) x z
0.8439500 -0.8755288 手元の計算機では、観測値が10万ぐらいないと識別できませんが、定義通り計算するより5倍ぐらい速いです。
4 従属変数の予測
推定された係数があれば、任意の説明変数の値に対応する従属変数の値を予測できます。coef(lm(...))に説明変数の値を乗じて足してもよいのですが、predict関数を使うのが簡便です。
1
4.114472 第2引数はデータフレームなので、複数の予測値を同時に出せます。
4.1 従属変数の予測区間
実際の作業としてはpredict関数に引数interval = "prediction"をつけるだけで計算できますが、予測区間は、観測値が予測値から外れる大きさが従う正規分布から求められ、以下のような演算が行なわれます。
観測値\(\tilde{y}\)と\(\tilde{x}\)と予測値\(\hat{y}\)の差、\(\{ \tilde{x}\beta + \epsilon \} - \{ \tilde{x} b \}\)を考えます。差の期待値は\(0\)です。\(\text{COV}(\tilde{y},\hat{y})=0\)なので、差の分散は\(\tilde{y}\)の分散と\(\hat{y}\)の分散の和になります。\(\tilde{y}\)の分散は\(\sigma^2\)にサンプルサイズの大きさの恒等行列を乗じて\(\sigma^2I\)になります。\(\hat{y}\)の分散は、推定量のベクトル\(b\)の分散と観測値の説明変数のベクトル\(\tilde{x}\)から、\(\tilde{x} \sigma^2 ({}^t\!XX)^{-1} {{}^t}\!\tilde{x}\)になります。期待値と分散が求まったので、t分布から区間推定を行ないます。
fit lwr upr
1 4.114472 1.865384 6.363559簡単ですね。predict関数を使わない場合は、以下のように計算できます。
X <- model.matrix(~ x + z, data = df01)
x <- model.matrix(~ x + z, data = df02)
se <- sqrt(diag(summary(r_lm)$sigma^2 * (diag(nrow(x)) + (x %*% (solve(t(X) %*% X)) %*% t(x)))))
a <- 0.05
margin <- qt(1 - a/2, 27) * se
sum(coef(r_lm) * x) + c(0, -margin, margin, use.names = FALSE)[1] 4.114472 1.865384 6.3635595 モデル選択
理屈だけではモデル選択が出来ない場合、当てはまりのよいモデルを選びます。モデル選択の方法は幾つかありますが、伝統的には分散分析、最近はクロスバリデーションの中でLOOCVが一般的のようです。
5.1 分散分析/F検定
2つのモデルを比較しますが、有意に異なる場合は複雑なモデルを採用します。
Analysis of Variance Table
Model 1: y ~ x + z
Model 2: y ~ x
Res.Df RSS Df Sum of Sq F Pr(>F)
1 27 18.755
2 28 80.340 -1 -61.585 88.657 5.083e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1ここではy ~ xよりもy ~ x + z、y ~ zよりもy ~ x + zが有意に予測力が高い事が示されています。
もちろん教科書的に検定を行なった場合と、結果は一致します。
F <- ((deviance(r_lm_r) - deviance(r_lm)) / (r_lm$rank - r_lm_r$rank)) / (deviance(r_lm) / r_lm$df.residual)
pf(F, r_lm$rank - r_lm_r$rank, r_lm$df.residual, lower.tail = FALSE)[1] 5.082933e-105.2 LOOCV
一つ抜き交差検証の名前の通りに計算した各モデルの誤差の大きさを比較します。bootパッケージのcv.glmを使うと手軽に実行できますが、cv.glmはlmの結果オブジェクトでは正常に動かないため、glm関数でOLS推定しています。
library(boot)
frml <- c("y ~ x", "y ~ z", "y ~ x + z")
delta <- matrix(NA, length(frml), 2)
rownames(delta) <- frml
colnames(delta) <- c("raw", "adjusted")
for(i in 1:length(frml)){
delta[i, ] <- cv.glm(df01, glm(formula(frml[i]), data=df01))$delta
}
print(delta) raw adjusted
y ~ x 3.0713661 3.0645320
y ~ z 2.5311366 2.5249000
y ~ x + z 0.7603282 0.7579476ここではy ~ x + zが最も誤差が小さいです。
6 プロット
推定量を示しても反応が薄い人々にインパクトを与えられたり、自分で自分の分析の誤りに気づく事もあるので、プロットは思ったよりも御利益があることが多いです。
6.1 回帰診断
推定結果のオブジェクトをplotすると、
- 予測値と残差
- 予測値と標準化残差の絶対値の平方根
- 正規Q–Q
- 梃子比(Leverage)と標準化残差の散布図とクック距離
の4つのプロットが順番に表示されます。
プロット領域を4分割し、ask = FALSEをつけて、一枚に納めて表示してみましょう3。
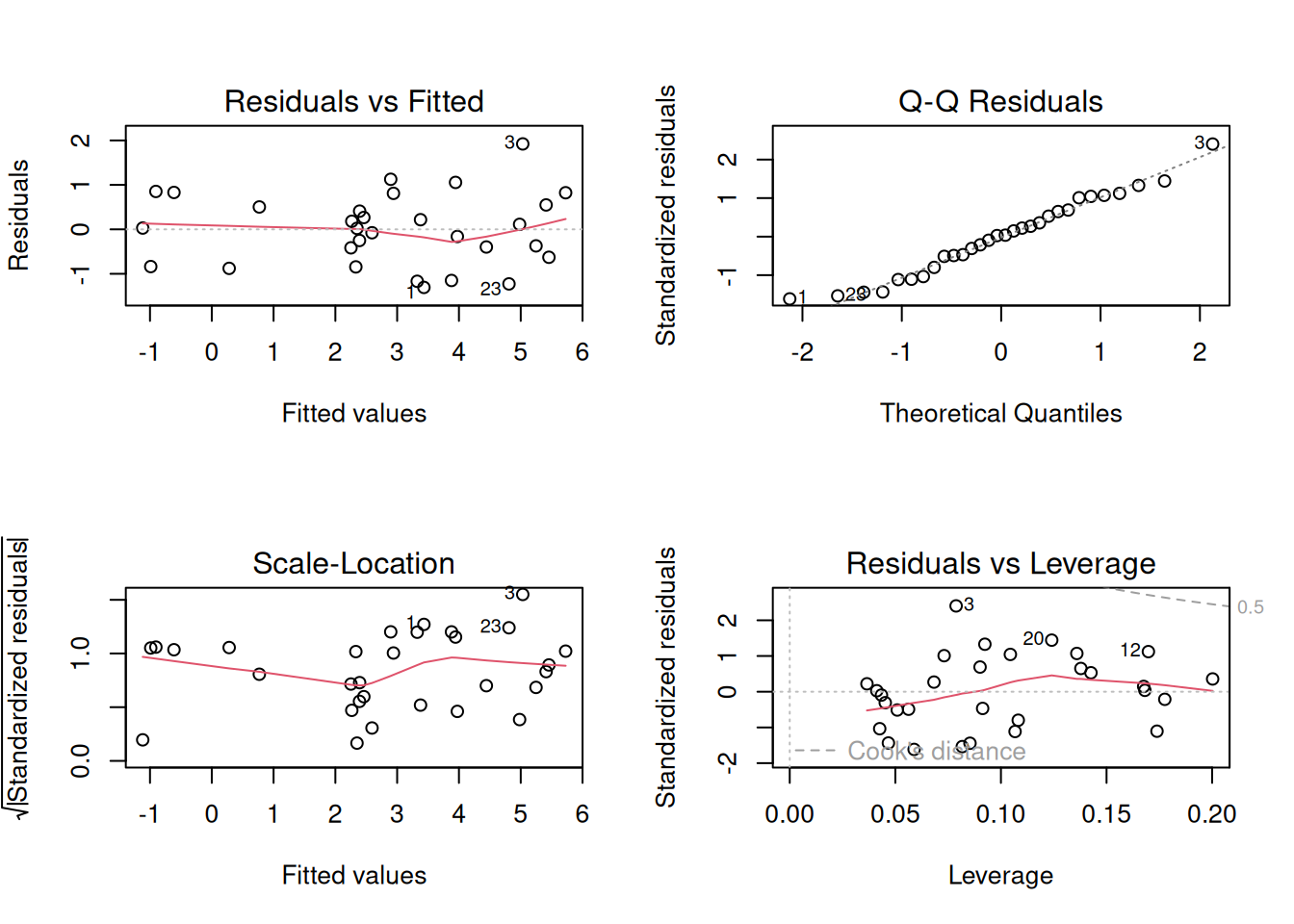
数字が入っていますが、データフレーム内の観測値の行番号を表します。行名がついている場合は、行名の表示になります。
予測値と残差や残差の散らばりに相関がある場合、極端なはずれ値がある場合は、推定モデルが不適切な可能性が高いです。
予測値と標準化残差の絶対値の平方根に相関がある場合は、OLSの残差を使った加重最小二乗法(FGLS)で推定しなおし、不均一分散に対処すべしとなります。
正規Q–Qプロットは、標準化残差を昇順に並べて分位数と標準化残差の対応をつくり、ある分位数における標準化残差を縦軸の座標、同じ分位数における標準化正規分布の確率変数(=標準化残差)を横軸の座標としたプロットです。だいたい斜めの直線上に並べば、残差が正規分布であると看做せます。
梃子比(Leverage)は観測値の回帰係数への影響が大きさをあらわす数値で、標準化残差と梃子比から計算したクック距離が多角なると、外れ値で回帰係数が偏っている可能性が高くなります。0.5や1.0が目安とされます。
観測値\(i\)の梃子比\(h_{ii}\)は
\[ h_{ii} \equiv {}^t\!x_i({}^t\!XX)^{-1}x_i \]
と定義され、\(0 \leq h_{ii} \leq 1\),\(\sum^n_{i=1}h_{ii}=k+1\),\(\bar{h}_{ii}=(k+1)/n\)となります。クック距離\(D_i\)は
\[ D_i \equiv \frac{e_i^2}{\hat{\sigma}^2}\frac{1}{k}\frac{h_{ii}}{(1-h_{ii})^2} \]
と定義されます。
なお、不偏性のある一致推定量を得るという意味では、誤差項が正規分布する必要も、分散が均一である必要もなく、系列相関も原則として支障になりません4。大標本のときは、梃子比を気にしましょう。
6.2 予測値
3変数以上ある場合はプロットに用いない変数の影響を除外するほうが、見栄えがよくなります。
# xの要素の昇順番を得る
i <- order(df01$x)
# zの効果を引き、zが平均値だった場合の効果を足したyをつくる
y <- with(df01, y - coef(r_lm)[3]*(z - mean(z)))
# xとyを昇順に並び替える
x <- df01$x[i]
y <- y[i]
# キャンバスの大きさを決める
xlim <- c(0, ceiling(max(x)))
ylim <- c(0, ceiling(max(y)))
# 白紙のキャンバスをつくる
par(mar = c(4, 4, 0.5, 0.5))
plot.new()
plot.window(xlim=xlim, ylim=ylim)
# 95%予測区間をピンク斜線で描く
px <- seq(xlim[1], xlim[2], length.out=100)
prdct <- predict(r_lm, data.frame(x = px, z = rep(mean(df01$z), length(px))), interval = "prediction")
px <- c(px, rev(px))
py <- c(prdct[,2], rev(prdct[,3]))
polygon(px, py, density=25, col="pink", border=NA)
# 予測線を描く
lines(xlim, predict(r_lm, data.frame(x = xlim, z = rep(mean(df01$z), 2))), lty = 3)
# 観測値をプロットする
points(x, y, pch=21, bg="white")
# 縦横軸ラベルを書く
title(
ylab = substitute(y - b*z + c, list(b = coef(r_lm)[3], c = mean(df01$z))),
xlab = expression(x)
)
# 軸を描く
axis(1)
axis(2)
6.3 信頼区間
dotchartは信頼区間を一覧するときに便利です。
ci <- confint(r_lm)
par(mar = c(4, 4, 0.5, 0.5))
dotchart(rev(coef(r_lm)), xlim = 1.2*range(ci),
cex = 1.25, labels = rev(rownames(ci)),
pch = 21, pt.cex = 1.5,
bg = "white", color = "black", lcolor = "darkgray")
arrows(ci[, 1], nrow(ci):1, ci[, 2], nrow(ci):1,
length = 0.1, angle = 90, code = 3)
